TEORIA DEI GRUPPI ED ORBITALI
Consideriamo una molecola con struttura appartenente al gruppo di simmetria D4h, cioè una struttura planare quadrata:
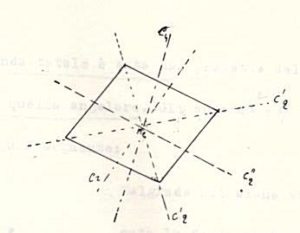 ad esempio PtCl4-2
ad esempio PtCl4-2 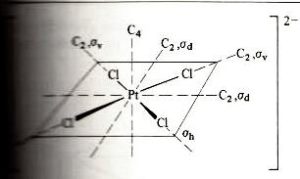
in cui gli orbitali hanno origine dal centro del quadrato .
Sappiamo che gli orbitali di tipo P per l’ atomo di idrogeno possiedono una parete radiale (che dipende da r ) ed una parte angolare (che dipende dagli angoli degli assi secondo coordinate cartesiane polari cioè gli angoli θ e Φ):

come si vede la parte radiale è identica per i 3 orbitali P mentre varia la parte angolare.
La funzione d’ onda è il prodotto tra la parte radiale e quella angolare e per atomi con più elettroni le proprietà di simmetria degli orbitali sono analoghe a quelle con un solo elettrone in quanto la parte angolare è uguale mentre la parte radiale differisce solo per le mutue azioni tra gli elettroni, quindi le conclusioni riguardanti la simmetria degli orbitali per un solo elettrone sono valide anche per atomi polielettronici. Questo significa che per gli atomi polielettronici possiamo usare gli orbitali relativi all’atomo monoelettronico.
Come è noto, queste funzioni sono soluzione dell’equazione di Schrodinger
HΨ =EΨ
dove H è l’ operatore Hamiltoniano che lascia la funzione immutata ma la moltiplica per una costante. Se le funzoni sono Px,Py,Pz avremo
HPx=E1Px
HPy=E2Py
HPz=E3Pz
Siccome i valori E1,E2,E3 sono uguali diciamo che le corrispondenti funzioni Px,Py,Pz sono “DEGENERI”.
Dal momento che sappiamo che effettuare un’operazione di simmetria su una molecola che appartiene ad un determinato gruppo di simmetria significa effettuare un’operazione sull’equazione d’onda che descrive ogni singolo orbitale dell’elemento centrale che lega altri atomi possiamo scrivere
XHPil = Ei Pil
Questa operazione di simmetria X può lasciare l’ orbitale nella medesima posizione originaria (si indica questo effetto con +1) oppure può modificarne la posizione ( si indica questo effetto con -1).
X Pi = ± 1Pi cioè
XHPi = HXPi = Ei (± 1Pi)
per gli orbitali degeneri come gli orbitali Px,Py,Pz non solo è valida la relazione sopra scritta ma è valida anche per una funzione orbitale nuova formata da una combinazione lineare dei suddetti orbitali (che è sempre soluzione dell’equazione di Schrodinger ) cioè:
Pil= a1Px+a2Py+a3Pz
dove a1,a2,a3 indicano la quantità di orbitale Px,Py e Pz che partecipa alla combinazione, quindi
XHPil = HXPil in cui XH =HX per cui si dice che gli operatori X ed H “commutano”.
XHPil = HXPil = EiPil
ed anche XPil= ∑3 j=1 xij Pij
Se effettuiamo una nuova operazione di simmetria B avremo
BPij = ∑3 m=1 bmij Pim
se effettuiamo prima l’operazione X e poi quella B avremo un’ operazione C che appartiene allo stesso gruppo di X e B
BXPil= CPil
CPil = B ∑3 j=1 xij Pij = ∑3 j=1 ∑3 m=1 bmj Xjl Pim
Cml = ∑3j=1 bmj Xij
La relazione sopra scritta non è altro che l’espressione analitica degli elementi di una matrice prodotto per cui se sottoponiamo le funzioni date ad operazioni di simmetria queste danno origine ad un gruppo. Vediamo adesso quali sono le matrici di trasformazione degli orbitali p.
La forma degli orbitali p in un complesso planare quadrato è
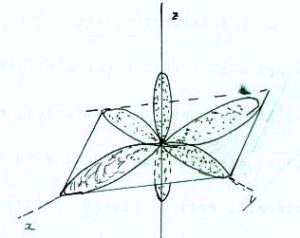
Agendo su questi orbitali con operazioni di simmetria D4h (poichè stiamo trattando una molecola planare quadrata ) avremo
1 ) l’orbitale può coincidere con la posizione da esso occupata prima dell’operazione (+1)
2) l’ orbitale può occupare una posizione diversa dall’originaria e può coincidere con un orbitale diverso. Ciò significa che per esempio se Px dopo l’operazione X occuoerà la posizione di Py si avrà la matrice :
In generale un orbitale si trasforma in altri due orbitali al massimo e ciò accade con le molecole a simmetria ottaedrica o tetraedrica (Oh e Td)
L’operazione identità del gruppo D4h lascia immutati i due orbitali Px e Py
EPx = +1 Px
EPy= +1 Py
in forma di matrice possiamo scrivere
La matrice di trasformazione ha quindi un carattere dato da χ = 1 +1 =2 χE=2
L’operazione C2 (rotazione intorno ad un asse C2) sposta i 2 orbitali verso la parte negativa degli assi quindi:
C2 Px= -1 Px
C2 Py = -1 Py in forma di matrice :
il carattere della matrice di trasformazione C2 = χ=-1 + -1 = -2 χ C2=-2
Delle due operazioni C’2 , la prima cambia di segno Px ma lascia immutato Py
C’2 Px= -Px
C’2 Py = Py cioè
il cui carattere è χ C’2=0
Le operazioni C”2 cambiano di segno Px che diventa -Py e Py che diviene – Px cioè
C”2 Px = -Py
C”2 Py = -Px
questo tipo di interazione è rappresentato dalla matrice seguente:
il primo termine
Il secondo integrale ∫ -PxPxdt = -1 in quanto sappiamo che ∫ψaψb dt =1 . In definitiva il carattere della trasformazione C2″ è :
il cui carattere è χ = 0
seguendo analogo ragionamento per tutte le operazioni del gruppo D4h si hanno i seguenti caratteri :
D4h E 2C4 C2 2C’2 2C”2 i 2S4 σh 2 σ v 2 σd
Px , Py 2 0 -2 0 0 -2 0 2 0 0
per lìorbitale Pz invece si ha
D4h E 2C4 C2 2C’2 2C”2 i 2S4 σh 2 σ v 2 σd
pz 1 1 1 -1 -1 -1 -1 -1 1 1
abbiamo così trovato le cosiddette “rappresentazioni riducibili” degli orbitali Px,Py,Pz.
Con lo stesso procedimento operiamo sugli orbitali d la cui espressione analitica è :

e la loro forma è
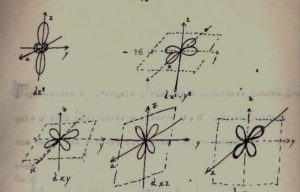
se consideriamo gli orbitali dxz e dyz otteniamo per l’operazione E che gli angoli θ e φ non vengono modificati quindi le funzioni rimangono inalterate ed in termini di matrice :
seguendo analogo procedimento troviamo che C2 lascia inalterato θ ma varia φ che diviene φ + π il che significa che tanto dxz che dyz variano di segno e quindi
l’operazione C2′ trasforma l’angolo θ in π – θ e l’angolo φ in – φ per cui l’orbitale dxz non viene modificato mentre si cambia di segno l’orbitale dyz
seguendo sempre questo procedimento per tutti gli orbitali osserviamo la seguente tavola dei caratteri riducibili
D4h E 2C4 C2 2C’2 2C”2 i 2S4 σh σv σd
dxz,dyz 2 0 -2 0 0 2 0 -2 0 0
dz2 1 1 1 1 1 1 1 1 1 1
dz2-y2 1 – 1 1 -1 -1 1 -1 1 -1 -1
dxy 1 -1 1 -1 1 1 -1 1 -1 1
se osserviamo la rappresentazione del gruppo D4h vediamo che dz2 si trasforma come A1g , dx2-y2 si trasforma come B1g, dxy come B2g, dxz e dyz come Eg mentre pz come A2u e Px,py come Eu.
Come è possibile notare, le Rappresentazioni irriducibili del gruppo sono state indicate con gli indici G ed u (gerade ed ungerade) che significano nel caso di g che la rappresentazione è simmetrica rispetto all’inversione ed nel caso di u è non simmetrica.Inoltre la lettera A indica rappresaentazioni di dimensione 1 e B invece di dimensione 2.
Ovviamente, il procedimento è valido per molecole con struttura ottaedrica o tetraedrica ma essendo piuttosto elaborato, useremo un metodo più semplice per ottenere i caratteri delle rappresentazioni Riducibili che poi ridurremo a quelle irriducibili semplicemente considerando quali orbitali rimangono in posizione invariata dopo l’operazione di simmetria.
Lascia un commento