Il calore di reazione non è altro che il calore emesso o acquistato in una reazione chimica. Il calore di reazione ΔHreaz è il risultato della differenza
∑ Hprodotti – ∑ Hreagenti = ΔHreaz
se la differenza produce un valore negativo significa che i prodotti possiedono un contenuto termico H più basso rispetto a quello dei reagenti e quindi durante la reazione si produce calore cioè si ha una reazione ESOTERMICA. Se invece i prodotti possiedono un contenuto termico maggiore rispetto ai reagenti, allora la differenza fornisce un valore positivo e la reazione avviene con assorbimento di calore cioè si ha una reazione ENDOTERMICA.
Essendo ΔH = Q possiamo quindi scrivere :
ΔH = – Q per una reazione esotermica essendo il ΔHreaz negativo (segno – perchè il sistema emette calore)
ΔH = Q per una reazione endotermica essendo ΔHreaz positivo (segno + perchè il sistema riceve calore)
I calori di reazione vengono spesso ottenuti sperimentalmente, ma per molte reazioni questo non è possibile per vari motivi tra cui vi è ad es. la formazione di composti indesiderati e quindi il valore misurato non corrisponde al valore reale. In questi casi si ricorre a calcoli che permettono di ottenere il ΔH di reazione ciò perchè sappiamo che ΔH è una funzione di stato che dipende dallo stato iniziale e da quello finale e non dalle modalità con cui si perviene allo stato finale.
In relazione a quanto sopra, la legge di Hess si può esprimere nel modo seguente:
"L'entalpia di una data reazione chimica è costante, sia che la reazione avvenga in
uno o in molti passaggi".
Un altro modo di esprimere la legge di Hess è:
"Se un'equazione chimica, può essere scritta come somma di diverse altre reazioni ,
la variazione di entalpia della prima equazione, è uguale alla somma delle variazio-
ni di entalpia delle altre equazioni chimiche".
Per fare un esempio consideriamo la reazione :
C (s) + ½ O2(g) = CO(g)
se utilizzassimo un calorimetro ad acqua per la combustione del C otterremmo un dato errato in quanto nella reazione di formerebbe anche CO2. Tuttavia, possiamo calcolare ugualmente il calore della reazione C (s) + ½ O2(g) = CO(g) in quanto sono noti i calori di combustione sia del C che del CO che si ottiene, infatti:
C(s) + O2(g)= CO2(g) ΔH = – 94.05 kcal/mol
CO(g) + ½ O2(g) = CO2(g) ΔH = – 67.41 kcal/mol
tornando alla reazione
C (s) + ½ O2(g) = CO(g) scriviamo i valori dei ΔH di combustione relativi
-94,05 → -67,41
poichè sappiamo che
∑ Hprodotti– ∑ Hreagenti = ΔHreaz
∑ ΔHprodotti– ∑ ΔHreagenti = ΔHreaz
si deduce che per la reazione data sopra si ha
ΔHreaz = – 94.05 kcal/mol – (– 67.41 kcal/mol) = – 94.05 + 67,41 = – 26.64 kcal/mol
infatti se scriviamo le reazioni
C(s) + O2(g) →CO2(g) C (s) + ½ O2(g) = CO(g)
CO2(g) →CO(g) + ½ O2(g) ΔH = +67.41 kcal/mol (essendo questa reazione l’inversa di quella di combustione)
se sommiamo le due reazioni e semplifichiamo, otteniamo
C (s) + ½ O2(g) = CO(g) ΔH= + 67.41 – – 94.05 =– 26.64 kcal/mol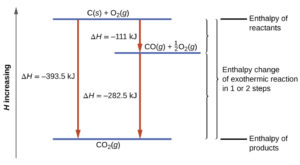
facciamo un altro esempio
calcoliamo il ΔH della trasformazione seguente:
| C (s, graphite) —> C (s, diamond) | ΔH° = ??? kJ |
avrai notato che sul ΔΗ vi è il simbolo ° cioè abbiamo scritto ΔΗ° ebbene esso indica che la trasformazione avviene in condizioni standard ed in questa discussione ometteremo il simbolo e indicheremo i ΔΗ° solo come ΔΗ.
La reazione di trasformazione del carbonio non può essere esaminata direttamente in laboratorio,questo perché, indipendentemente dalla bassa entalpia, la reazione richiede
un’energia di attivazione molto alta per far partire la reazione. La conseguenza è che il valore dell’entalpia non può essere determinato direttamente in quasi tutti i laboratori e, in quelli che possono farlo il processo è molto, molto difficile.La legge di Hess permette tuttavia di calcolare il ΔΗ.Infatti si conoscono le entalpie delle equazioni
| C (s, graphite) + O2(g) —> CO2(g) | ΔH° = -393.5 kJ |
| C (s, diamond) + O2(g) —> CO2(g) | ΔH° = -395.4 kJ |
se invertiamo la seconda reazione e cambiamo ovviamente il segno di ΔΗ avremo
| C (s, graphite) + O2(g) —> CO2(g) | ΔH° = -393.5 kJ |
| CO2(g) —> C (s, diamond) + O2(g) | ΔH° = +395.4 kJ |
se sommiamo membro a membro le due equazioni
C (s, graphite) + O2(g) + CO2(g) –>C (s, diamond) + O2(g) + CO2(g) ΔΗ = -393.5 kJ +395.4 kJ
semplificando si ha proprio la reazione iniziale di cui volevamo conscere il ΔΗ:
C (s, graphite) —> C (s, diamond) quindi il ΔΗ = -393.5 kJ +395.4 kJ = + 1,9 kJ
L’applicazione della Legge di Hess permette il calcolo di ΔHreaz se si conoscono ad esempio i ΔHdi formazione dei partecipanti ad una reazione. Per esempio sia la reazione:
Calcola l'entalpia per questa reazione
| 2C(s) + H2(g) —> C2H2(g) | ΔH° = |
Date le seguenti equazioni termochimiche di cui sono noti i calori di formazione:
| C2H2(g) + 5⁄2O2(g) —> 2CO2(g) + H2O(ℓ) | ΔH° = -1299.5 kJ |
| C(s) + O2(g) —> CO2(g) | ΔH° = -393.5 kJ |
| H2(g) + 1⁄2O2(g) —> H2O(ℓ) | ΔH° = -285.8 kJ |
Cosa dobbiamo fare alle tre equazioni date per ottenere la nostra equazione
finale?
a) prima equazione: riscriverla in modo da mettere C2H2 sul lato del prodotto
b) seconda equazione : moltiplicarla per due per ottenere 2C
c) terza equazione : non fare nulla. Abbiamo bisogno di un H2 sul lato del reagente
2) riscriviamo le reazioni
2CO2(g) + H2O(ℓ) —> C2H2(g) + 5⁄2O2(g) ΔH° = +1299.5 kJ 2C(s) + 2O2(g) —> 2CO2(g) ΔH° = -787 kJ H2(g) + 1⁄2O2(g) —> H2O(ℓ) ΔH° = -285.8 kJ nota che il valore di ΔΗ della prima reazione è cambiato di segno.
Sommando e semplificando si ha:
2C(s) + H2(g) —> C2H2(g) da cui ricordando che
∑ Hprodotti – ∑ Hreagenti = ΔHreaz
+1299.5 kJ – 787 kJ) – 285.8 kJ) = ΔΗ= +226.7 kJ
ancora un esempio
data la seguente reazione calcolare ΔΗ
CS2(ℓ) + 3O2(g) —> CO2(g) + 2SO2(g)
conoscendo i seguenti dati:
C(s) + O2(g) —> CO2(g) ΔH = -393.5 kJ/mol S(s) + O2(g) —> SO2(g) ΔH = -296.8 kJ/mol C(s) + 2S(s) —> CS2(ℓ) ΔH = +87.9 kJ/mol soluzione
lasciamo intatta l'eq 1 (infatti CO2 è un prodotto) moltiplica la seconda eq per 2 ( 2SO2 dal lato del prodotto) inverti la terza equazione (infatti CS2 è il reagente) eseguendo le operazioni sopra indicate sulle 3 equazioni date, e sommandole semplificando si ha
C(s) + O2(g) —> CO2(g) ΔH = -393.5 kJ/mol 2S(s) + 2O2(g) —> 2SO2(g) ΔH = -593.6 kJ/mol <— note multiply by 2 on the ΔH CS2(ℓ) —> C(s) + 2S(s) ΔH = -87.9 kJ/mol <— note sign change on the ΔH cioè CS2(ℓ) + 3O2(g) ---> CO2(g) + 2SO2(g) che è l'equazione di cui vogliamo calcolare ΔΗ pertanto possiamo scrivere ricordando che ∑ Hprodotti - ∑ Hreagenti = ΔHreaz -393,5 - 593,6 - (-87,9 ) = ΔHreaz = -899,2 kJ/mol altro esempio dai seguenti dati:
SrO(s) + CO2(g) —> SrCO3(s) ΔH = -234 kJ 2SrO(s) —> 2Sr(s) + O2(g) ΔH = +1184 kJ 2SrCO3(s) —> 2Sr(s) + 2C(s, gr) + 3O2(g) ΔH = +2440 kJ calcola il ΔH della seguente reazione:
C(s, gr) + O2(g) —> CO2(g)
soluzione
invertiamo la prima reazione data in modo che CO2 si trovi a destra della reazione
SrO(s) + CO2(g) —> SrCO3(s) ΔH = -234 kJ SrCrO3 → SrO + CO2 ΔH = + 234 kJ (cambia di segno) lasciamo invariata la seconda
2SrO(s) —> 2Sr(s) + O2(g) ΔH = +1184 kJ invertiamo la terza perchè C deve essere a sinistra nella reazione e si ha
2Sr(s) +2 C(s, gr) + 3O2(g) —> 2SrCO3(s) ΔH = -2440 kJ ma siccome a sinistra vi deve essere solo un atomo di C allora quest'ultima reazione la dividiamo per 2 ed otteniamo
Sr(s) + C(s, gr) + 3⁄2O2(g) —> SrCO3(s) ΔH = -1220 kJ in definitiva abiamo le tre reazioni
SrCO3(s) —> SrO(s) + CO2(g) ΔH = +234 kJ SrO(s) —> Sr(s) + 1⁄2O2(g) ΔH = +592 kJ Sr(s) + C(s, gr) + 3⁄2O2(g) —> SrCO3(s) ΔH = -1220 e sommando membro a membro e semplificando si ha : C(s, gr) + O2(g) ---> CO2(g) ΔΗ = 234 +592 - 1220 =-394 kj che è il calore di formazione di CO2 ancora un esempiodai seguenti dati
2NO(g) + O2(g) —> 2NO2(g) ΔH = -116 kJ 2N2(g) + 5O2(g) + 2H2O(ℓ) —> 4HNO3(aq) ΔH = -256 kJ N2(g) + O2(g) —> 2NO(g) ΔH = +183 kJ calcolare ΔΗ per la seguente reazione:
3NO2(g) + H2O(ℓ) —> 2HNO3(aq) + NO(g) ΔH = ??? Solution:
1) analizziamo ciò che dobbiamo fare:
a) invertiamo la prima reazione e moltiplichiamo per 3⁄2 (questo fornisce 3NO2 e 3NO che sono necessari per ottenere NO nella risposta finale)b) dividere la seconda equazione per 2 (il che ci fornisce 2 HNO3 nella risposta finale)
c) invertiamo la terza equazione (il che cancella 2NO così come N2)
2) osserviamo l’ossigeno:
a) secondo il punto 1a 3⁄2O2 saranno sulla destra
b) secondo il punto 1b 5⁄2O2 saranno a sinistra
c) secondo il punto 1c 2⁄2O2 saranno sulla destraInoltre a e c danno 5⁄2O2 sulla destra per cancellare 5⁄2O2 sulla sinistra
3) Applicando quanto detto sopra
3NO2(g) —> 3NO(g) + 3⁄2O2(g) ΔH = +174 kJ N2(g) + 5⁄2O2(g) + H2O(ℓ) —> 2HNO3(aq) ΔH = -128 kJ 2NO(g) —> N2(g) + O2(g) ΔH = -183 kJ 4) sommare le reazioni ed il ΔΗ:
+174 + (-128) + (-183) = -137 kJ
3NO2(g) + H2O(ℓ) —> 2HNO3(aq) + NO(g) ΔH = -137 kJ altro esempio
calcolare il ΔΗ della reazione
CH4(g) + NH3(g) —> HCN(g) + 3H2(g)
dai dati seguenti:
N2(g) + 3 H2(g) —> 2 NH3(g) ΔH = -91.8 kJ C(s) + 2 H2(g) —> CH4(g) ΔH = -74.9 kJ H2(g) + 2 C(s) + N2(g) —> 2 HCN(g) ΔH = +270.3 kJ Solutione:
1) effettuiamo le azioni sulle reazioni date:
a)invertire l’equazione 1 e dividerla per 2 ( questo pone NH3 sul lato dei reagenti)
b) invertiamo la seconda equazione (questo pone CH4 sul lato dei reagenti)
c) dividiamo peer 2 la terza equazione (pone HCN sul lato dei prodotti)2) Riscriviamo pertanto le reazioni ottenute dopo le operazioni fatte sopra:
NH3(g) —> 1⁄2N2(g) +3⁄2H2(g) ΔH = +45.9 kJ (il segno è cambiato e si è diviso per 2) CH4(g) —> C(s) + 2 H2(g) ΔH = +74.9 kJ il segno è cambiato 1⁄2H2(g) + C(s) + 1⁄2N2(g) →HCN(g) ΔH = +135.15 kJ si è diviso per 2 3) sommando le equazioni e semplificando otteniamo:
CH4(g) + NH3(g) —> HCN(g) + 3H2(g)4) Calcoliamo adesso il ΔH :
+45.9 kJ +74.9 kJ +135.15 = 255.95 kJ = 260. kJ (nota che le cifre significative devono essere solo 3 per cui 255,95 è approssimato a 256 e quindi a 260)
altro esempio
calcolare il ΔΗ per la reazione seguente :
NO2(g) + 7⁄2H2(g) —> 2H2O(ℓ) + NH3(g)
dai seguenti dati:
2NH3(g) —> N2(g) + 3H2(g) ΔH° = +92 kJ
1⁄2N2(g) + 2H2O(ℓ) —> NO2(g) + 2H2(g) ΔH° = +170 kJ
Soluzione
consideriamo la prima reazione ed osserviamo che dobbiamo considerare solo una molecola di NH3 in quanto nella reazione con ΔΗ incognito compare solo una volta infatti la reazione è:
NO2(g) + 7⁄2H2(g) —> 2H2O(ℓ) + NH3(g)
pertanto
2NH3(g) —> N2(g) + 3H2(g) ΔH° = +92 kJ
deve essere riscritta :
1⁄2N2(g) + 3⁄2H2(g) —> NH3(g) ΔH° = -46 kJ
(nota che abbiamo diviso per 2 ed invertito la reazione !)
la seconda reazione
1⁄2N2(g) + 2H2O(ℓ) ---> NO2(g) + 2H2(g) dev'essere invertita perché nella reazione a ΔΗ incognito NO2 compare a sinistra perciò la riscriviamo: NO2(g) + 2H2(g) ---> 1⁄2N2(g) + 2H2O(ℓ) ΔH° = -170 kJ adesso sommiamo le due reazioni e semplifichiamo e sommiamo anche i ΔH ed otteniamo: NO2(g) + 7⁄2H2(g) ---> 2H2O(ℓ) + NH3(g) ΔΗ= -46 + -170 = -216 kJancora un esempio calcolare il ΔΗ per la reazione: N2(g) + 2O2(g) ---> 2NO2(g) dai seguenti dati: N2(g) + O2(g) ---> 2NO(g) ΔH° = +180 kJ 2NO2(g) ---> 2NO(g) + O2(g) ΔH° = +112 kJ soluzione la prima reazione deve rimanere immutata in quanto N2 compare a sinistra nella reazione a ΔΗ incognito perciò N2(g) + O2(g) ---> 2NO(g) ΔH° = +180 kJ La seconda reazione 2NO2(g) ---> 2NO(g) + O2(g) invece va invertita perchè NO2 nella reazione a ΔΗ incognito si trova a destra pertanto: 2NO(g) + O2 --> 2NO2 ΔΗ = - 112 kJ sommando le due reazioni riscritte e semplificando si ha N2(g) + 2O2(g) ---> 2NO2(g) ΔΗ = - 112 kJ + 180 kJ = 68 KJ /mol ancora esempi dai seguenti dati : 2NO(g) ---> N2(g) + O2(g) ΔH = -180.6 kJ N2(g) + O2(g) + Cl2(g) ---> 2NOCl(g) ΔH = +103.4 kJ calcolare il ΔΗ per la reazione2NOCl(g) —> 2NO(g) + Cl2(g)
soluzione
sia la prima reazione che la seconda devono essere invertite in quanto Cl2 ed NO si trovano a destra della reazione con ΔΗ incognito
N2(g) + O2(g) —> 2NO(g) ΔH = +180.6 kJ
2NOCl(g) —> N2(g) + O2(g) + Cl2(g) ΔH = -103.4 kJ
sommando e semplificando si ottiene
2NOCl(g) —> 2NO(g) + Cl2(g) ΔΗ = +180.6 + (-103.4) = +77.2
altro esercizio
Il carbon suboxido, C3O2,è un gas a temperatura ambiente is a gas at room temperature. Usa i dati forniti per calcolare il calore di formazione del carbon suboxido.
2CO(g) + C(s) —> C3O2(g) ΔH° = +127.3 kJ CO(g) ΔH°f = -110.5 kJ Soluzione:
1) la reazione di formazione del subossido è :
3C(s) + O2(g) —> C3O2(g)
2) scriviamo la reazione di formazione del CO:
C(s) + 1⁄2O2(g) —> CO(g) ΔH°f = -110.5 kJ
moltiplichiamo per 2 (per cancellare 2CO quando si sommeranno le reazioni)
2C(s) + O2(g) —> 2CO(g) ΔH = -221.0 kJ
3) scrivere le due reazioni da sommare:
2CO(g) + C(s) —> C3O2(g) ΔH° = +127.3 kJ
2C(s) + O2(g) —> 2CO(g) ΔH = -221.0 kJ
sommiamo, semplifichiamo ed otteniamo
3C(s) + O2(g) —> C3O2(g) ΔΗf = +127.3 kJ + (-221.0 kJ)
ΔΗf = – 93.7 kJ
Esempio ulteriore
Durante la scarica di una batteria di accumulatori al piombo, si verifica la seguente reazione chimica:
Pb + PbO2 + 2H2SO4 —> 2PbSO4 + 2H2O
Using the following two reactions:
(1) Pb + PbO2 + 2SO3 —> 2PbSO4 ΔH° = -775 kJ
(2) SO3 + H2O —> H2SO4 ΔH° = -775 kJ
Determinare l'entalpia della reazione di scarica sopra scritta Soluzione :1) moltiplicare l’ equazione (2) per 2:
2SO3 + 2H2O —> 2H2SO4 ΔH = -226 kJ
2)invertiamo reagenti e prodotti nella reazione (2). Il segno dell’entalpia diviene positivo. come vediamo nell’equazione (3):
(3) 2H2SO4 —> 2SO3 + 2H2O ΔH° = 226 kJ
3) sommare le equazioni (1) e (3):
Pb + PbO2 + 2SO3 + 2H2SO4 —> 2PbSO4 + 2SO3 + 2H2O
4) sommare le entalpie delle equazioni (1) e (3):
Pb + PbO2 + 2H2SO4 —> 2PbSO4 + 2H2O ΔH° = -549 kJ
ancora esempi
Le variazioni entalpiche standard della combustione di glucosio ed etanolo sono rispettivamente -2820 e -1368 kJ mol¯ Il Glucosio, C6H12O6, può essere convertito in etanolo.C6H12O6(s) —> 2C2H5OH(ℓ) + 2CO2(g)
calcolare la variazione di entalpia per questa reazione.
Soluzione:
1) scrivere le reazioni di combustione del glucosio e dell’etanolo
C6H12O6(s) + 6O2(g) —> 6CO2(g) + 6H2O(ℓ) ΔH = -2820 kJ
C2H5OH(ℓ) + 3O2(g) —> 2CO2(g) + 3H2O(ℓ) ΔH = -1368 kJ
2) inertire la reazione 2 e moltiplichiamo per 2
4CO2(g) + 6H2O(ℓ) —> 2C2H5OH(ℓ) + 6O2(g) ΔH = +2736 kJ
sommiamo e semplifichiamo ed otteniamo:
C6H12O6(s) —> 2C2H5OH(ℓ) + 2CO2(g) ΔH = -84 kJ
esempio
Determinare il calore di reazione per l’ossidazione del ferro:
2Fe(s) + 3⁄2O2(g) —> Fe2O3(s)
date le seguenti reazioni:
2Fe(s) + 6H2O(ℓ) —> 2Fe(OH)3(s) + 3H2(g) ΔH = +322 kJ
e2O3(s) + 3H2O(ℓ) —> 2Fe(OH)3(s) ΔH = +289 kJ
2H2(g) + O2(g) —> 2H2O(ℓ) ΔH = 572 kJ
Soluzione:
lasciamo inalterata la prima reazione
2Fe(s) + 6H2O(ℓ) —> 2Fe(OH)3(s) + 3H2(g) ΔH = +322 kJ
invertiamo la seconda reazione
2Fe(OH)3(s) —> Fe2O3(s) + 3H2O(ℓ) ΔH = -289 kJ
moltiplichiamo la terza reazione per 3/2
3H2(g) + 3⁄2O2(g) —> 3H2O(ℓ) ΔH = –858 kJ
sommiamo le reazioni e semplifichiamo ottenendo
2Fe(s) + 3⁄2O2(g) —> Fe2O3(s) ΔH = -825 kJ
Problema #1:
I calori di combustione di C, H2 e CH4 a 298 K e 1 atm sono rispettivamente -393 kJ / mol, -286 kJ / mol e -892 kJ / mol.
Qual è l'entalpia di formazione di CH4 ?Soluzione:
1) le reazioni sono
C + O2 —> CO2 ΔH = -393 kJ
H2 + 1⁄2O2 —> H2O ΔH = -286 kJ
CH4 + 2O2 —> CO2 + 2H2O ΔH = -892 kJ
la reazione di formazione del metano CH4 è :
C + 2H2 —> CH4lasciamo inalterata la reazione 1
dividiamo la seconda per 2
invertiamo la terza reazione
sommando e semplificando si ha
C + 2H2 —> CH4 Δ Ηf = (-393) + 2(-286) + 892) = -393 – 572 + 892= 73 KJ/mol
problema 2
Il calore standard di combustione del benzene è -3271 kJ / mol, per CO2 è -394 kJ / mol e per H2O è -286 kJ / mol. Calcola il calore standard di formazione del benzene. soluzione la reazione di combustione del benzene è: C6H6 + 15⁄2O2 ---> 6CO2 + 3H2O ΔH = -3271 kJ l'entalpia di formazione del benzene può essere calcolata ricordando cheΔΗreaz = ∑prodotti – ∑reagenti possiamo scrivere
-3271 = [(6) (-394) + (3) (-286)] – [ΔΗC6H6 + (15/2) (0)]
da cui ΔΗC6H6 = 49 kJ/mol
Problema #3:
I calori di combustione per l’idrogeno metano ed etano sono rispettivamente
-285.8, -890.4 e -1559.9 kJ/mol a 298K. Calcolare ( alla stessa temperatura)il calore di reazione della seguente reazione:
2CH4(g) —> C2H6(g) + H2(g)
Soluzione:
sappiamo che :
H2 + 1⁄2O2 ---> H2O ΔH = -285.8 kJCH4 + 2O2 —> CO2 + 2H2O ΔH = -890.4 kJ
C2H6 + 7⁄2O2 —> 2CO2 + 3H2O ΔH = -1559.9 kJ
invertiamo la prima reazione perchè l’H è un prodotto della reazione di cui intendiamo ottenere il ΔΗ
moltiplichiamo per 2 la seconda reazione per ottenere 2 CH4
invertiamo la terza per ottenere C2H6 come prodotto
H2O —> H2 + 1⁄2O2 ΔH = +285.8 kJ
2CH4 + 4O2 —> 2CO2 + 4H2O ΔH = -1780.8 kJ
2CO2 + 3H2O —> C2H6 + 7⁄2O2 ΔH = +1559.9 kJ
sommando e semplificando si ha :
2CH4(g) —> C2H6(g) + H2(g) ΔΗreaz. = +1559,9 + (- 1780,8) + 285,8 ΔΗreaz.=64,9 KJ
Problema 4:
Calcolare l’entalpia standard per la riduzione dell’ossido di Fe(II) con CO dai seguenti dati:
FeO(s) + CO(g) —> Fe(s) + CO2(g)
3Fe2O3(s) + CO(g) —> 2Fe3O4(s) + CO2(g) ΔH = -48.26 kJ
Fe2O3(s) + 3CO(g) —> 2Fe(s) + 3CO2(g) ΔH = -23.44 kJ
Fe3O4(s) + CO(g) —> 3FeO(s) + CO2(g) ΔH = +21.79 kJ
soluzione
invertiamo l’equazione 1 in modo da avere Fe3O4 sul lato sinistro
moltiplichiamo l’equazione 2 per 3 in modo da avere 3Fe2O3
invertiamo la reazione 3 e moltiplichiamo per 2
2Fe3O4(s) + CO2(g) —> 3Fe2O3(s) + CO(g) ΔH = +48.26 kJ
3Fe2O3(s) + 9CO(g) —> 6Fe(s) + 9CO2(g) ΔH = -70.32 kJ
6FeO(s) + 2CO2(g) —> 2Fe3O4(s) + 2CO(g) ΔH = -43.58 kJ
sommando queste reazioni si ha
6FeO(s) + 6CO(g) —> 6Fe(s) + 6CO2(g)
l’entalpia di reazione è : ΔΗreaz. = +48.26 + (-70.32) + (-43.58) = -65.64 kJ
Problema 5:
Calcolare l’entalpia per la seguente reazione:
2C(s) + H2(g) —> C2H2(g) ΔH° = ??? kJ sapendo che :
C2H2(g) + 5⁄2O2(g) —> 2CO2(g) + H2O(ℓ) ΔH° = -1299.5 kJ C(s) + O2(g) —> CO2(g) ΔH° = -393.5 kJ H2(g) + 1⁄2O2(g) —> H2O(ℓ) ΔH° = -285.8 kJ Soluzione
a)invertiamo la prima reazione in modo da mettere C2H2 sul lato dei prodotti
b) moltiplicare per due la seconda reazione per ottenere 2C
c)lasciamo intatta la terza reazione2) Riscriviamo tutte e tre le reazioni con le modifiche applicate:
2CO2(g) + H2O(ℓ) —> C2H2(g) + 5⁄2O2(g) ΔH° = +1299.5 kJ 2C(s) + 2O2(g) —> 2CO2(g) ΔH° = -787 kJ H2(g) + 1⁄2O2(g) —> H2O(ℓ) ΔH° = -285.8 kJ Notice that the ΔH values changed as well.
3) semplifichiamo le quantità dei reagenti e prodotti
2CO2
H2O
5⁄2O24) sommiamo i valori di ΔH ed otteniamo la risposta al quesito
+1299.5 kJ + (-787 kJ) + (-285.8 kJ) = +226.7 kJ
esempio 6 : Calcolare l’entalpia per la reazione::
CS2(ℓ) + 3O2(g) —> CO2(g) + 2SO2(g)
sapendo che :
C(s) + O2(g) —> CO2(g) ΔH = -393.5 kJ/mol S(s) + O2(g) —> SO2(g) ΔH = -296.8 kJ/mol C(s) + 2S(s) —> CS2(ℓ) ΔH = +87.9 kJ/mol Soluzione:
lasciamo immutata la reazione 1 ( CO2 infatti compare tra i prodotti)
moltiplichiamo per 2 la seconda reazione ( 2SO2 si ha così sul lato dei prodotti)
invertire la terza reazione ( CS2 deve comparire tra i reagenti)
C(s) + O2(g) —> CO2(g) ΔH = -393.5 kJ/mol 2S(s) + 2O2(g) —> 2SO2(g) ΔH = -593.6 kJ/mol CS2(ℓ) —> C(s) + 2S(s) ΔH = -87.9 kJ/mol semplifichiamo e sommiamo
ΔH = -393.5 + (-593.6 ) + ( -87.9 ) = 1075 kJ/mol
Problema 7:
date le seguenti reazioni:
SrO(s) + CO2(g) —> SrCO3(s) ΔH = -234 kJ 2SrO(s) —> 2Sr(s) + O2(g) ΔH = +1184 kJ 2SrCO3(s) —> 2Sr(s) + 2C(s, gr) + 3O2(g) ΔH = +2440 kJ trovare il ΔHformazione per la CO2 nella seguente reazione:
C(s, gr) + O2(g) —> CO2(g)
Soluzione:
a invertiamo la prima reazione per avere CO2 sul lato destrob) dividiamo la seconda reazione per 2
c) invertire al terza reazione per avere SrCO3 sul lato destro e dividere per 2 in quanto dobbiamo cancellare solo una molecola di SrCO3
avremo:
SrCO3(s) —> SrO(s) + CO2(g) ΔH = +234 kJ SrO(s) —> Sr(s) + 1⁄2O2(g) ΔH = +592 kJ Sr(s) + C(s, gr) + 3⁄2O2(g) —> SrCO3(s) ΔH = -1220 kJ si eliminano
SrCO3, SrO, Sr, 1⁄2O2
4) sommiamo i valori di ΔH :
+234 + (+592) + (-1220) = -394
C(s, gr) + O2(g) —> CO2(g) ΔH°f = -394 kJ
Problema 8: sapendo che :
2NO(g) + O2(g) —> 2NO2(g) ΔH = -116 kJ 2N2(g) + 5O2(g) + 2H2O(ℓ) —> 4HNO3(aq) ΔH = -256 kJ N2(g) + O2(g) —> 2NO(g) ΔH = +183 kJ Calcolare la variazione di entalpia per la reazione:
3NO2(g) + H2O(ℓ) —> 2HNO3(aq) + NO(g) ΔH = ??? Soluzione :
a) invertiamo la prima reazione e moltiplichiamola per 3⁄2
(b) dividere la seconda reazione per 2
c) invertire la terza reazione ) per quanto attiene l’ossigeno
a) il primo punto porta 3⁄2O2 sul lato destro
b) il punto secondo pone 5⁄2O2 a sinistra
c) il terzo pone 2⁄2O2 sulla destra i punti a and c forniscono 5⁄2O2 sulla destra che si cancella con 5⁄2O2 sulla sinistra)ne consegue che:
3NO2(g) —> 3NO(g) + 3⁄2O2(g) ΔH = +174 kJ N2(g) + 5⁄2O2(g) + H2O(ℓ) —> 2HNO3(aq) ΔH = -128 kJ 2NO(g) —> N2(g) + O2(g) ΔH = -183 kJ 4) sommando si ha ΔH
ΔΗ= +174 + (-128) + (-183) = -137 kJ
3NO2(g) + H2O(ℓ) —> 2HNO3(aq) + NO(g) ΔH = -137 kJ
Problema 9 :
Calcolare ΔH per la reazione:
CH4(g) + NH3(g) —> HCN(g) + 3H2(g)
sapendo che :
N2(g) + 3 H2(g) —> 2 NH3(g) ΔH = -91.8 kJ C(s) + 2 H2(g) —> CH4(g) ΔH = -74.9 kJ H2(g) + 2 C(s) + N2(g) —> 2 HCN(g) ΔH = +270.3 kJ Soluzione:
a) invertiamo la prima reazione e dividiamola per 2 f (NH3 sarà adesso a destra)
b)invertiamo la seconda reazione (CH4 sarà sul lato destro)
c) dividiamo la terza reazione per 2 ( HCN sarà sul lato dei prodotti)avremo:
NH3(g) —> 1⁄2N2(g) + 3⁄2H2(g) ΔH = +45.9 kJ CH4(g) —> C(s) + 2 H2(g) ΔH = +74.9 kJ 1⁄2H2(g) + C(s) + 1⁄2N2(g) —> HCN(g) ΔH = +135.15 kJ sommiamo e semplifichiamo ed otteniamo ΔH della reazione:
ΔΗ = +45.9 kJ plus +74.9 kJ plus +135.15 = 255.95 kJ = 260. kJ
Problema 10:
calcolare l’entalpia standard di combustione di 1 mole di acetone liquido (C3H6O) sapendo che :
3C(s) + 3H2(g) + 1⁄2O2(g) —> C3H6O(ℓ) ΔH° = -285.0 kJ C(s) + O2(g) —> CO2(g) ΔH° = -394.0 kJ H2(g) + 1⁄2O2(g) —> H2O(ℓ) ΔH° = -286.0 kJ Soluzione:
la reazione di combustione dell’acetone è:
C3H6O(ℓ) + 4O2(g) —> 3CO2(g) + 3H2O(ℓ)
invertiamo la prima delle reazioni date e lasciamo inalterate le altre.
C3H6O(ℓ) —> 3C(s) + 3H2(g) + 1⁄2O2(g) ΔH° = +285.0 kJ C(s) + O2(g) —> CO2(g) ΔH° = -394.0 kJ H2(g) + 1⁄2O2(g) —> H2O(ℓ) ΔH° = -286.0 kJ
moltiplichiamo per 3 la seconda reazione
C3H6O(ℓ) —> 3C(s) + 3H2(g) + 1⁄2O2(g) ΔH° = +285.0 kJ 3C(s) + 3O2(g) —> 3CO2(g) ΔH° = -1182.0 kJ H2(g) + 1⁄2O2(g) —> H2O(ℓ) ΔH° = -286.0 kJ moltiplichiamo per 3 la terza reazione
C3H6O(ℓ) —> 3C(s) + 3H2(g) + 1⁄2O2(g) ΔH° = +285.0 kJ 3C(s) + 3O2(g) —> 3CO2(g) ΔH° = -1182.0 kJ 3H2(g) + 3⁄2O2(g) —> 3H2O(ℓ) ΔH° = -858.0 kJ sommiamo e semplifichiamo ed otteniamo per la reazione data
C3H6O(ℓ) + 4O2(g) —> 3CO2(g) + 3H2O(ℓ)
ΔΗ =+285.0 -1182.0 -858.0 = -1755 k
Lascia un commento