ELETTROCHIMICA: GLI ELETTRODI

IL POTENZIALE DI OSSIDO-RIDUZIONE

Se consideriamo una lamina di metallo M immersa in una soluzione dei suoi ioni M⁺ⁿ

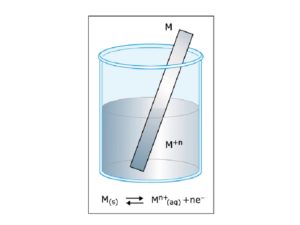
si osservano 2 processi : il passaggio del metallo M in soluzione sotto forma dei suoi ioni M→ M⁺ⁿ+ n e e contemporaneamente il depositarsi degli ioni M⁺ⁿsulla lamina di metallo M⁺ⁿ+ ne→ M. Si raggiungerà quindi uno stato di equilibrio:

Ms ⇄ M⁺ⁿ_aq+ ne

dove ne sono gli elettroni scambiati all’interfaccia Metallo-soluzione.

Durante il passaggio in soluzione, sulla superficie della lamina rimangono gli n elettroni e quindi si determina tra la lamina di metallo e la soluzione acquosa un doppio strato elettrico con opposte cariche . La figura mostra una lamina di magnesio immersa in una soluzione acquosa

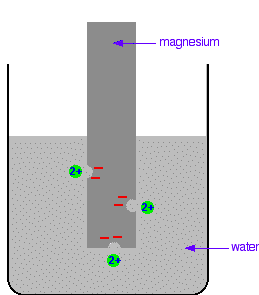
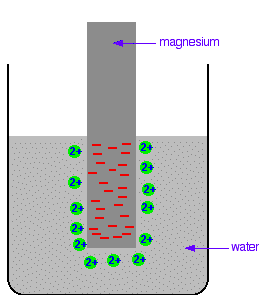
Il Mg forma ioni Mg+2 acquoso e sulla lamina rimangono due cariche elettriche cioè 2 elettroni. Come conseguenza di questa separazione di cariche, nell’interfaccia Metallo-soluzione si determina una differenza di potenziale elettrico che si indica con E.

Riassumendo : quando un solido è immerso in un liquido polare si carica elettricamente in superficie. In genere la carica è negativa. Tale carica causa la formazione di una struttura denominata “doppio strato elettrico”. Le cariche negative superficiali attraggono gli ioni positivi solvatati e orientano le molecole costituenti il liquido. Ioni e molecole generano quindi un cuscinetto ordinato di cariche sulla superficie del solido, via via sempre più diffuso verso il resto del liquido. Si distinguono quindi sulla superficie del solido:

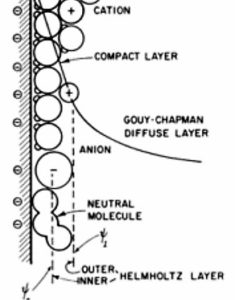
a) uno strato carico negativamente (Outer + Inner strato di Helmholtz);

b) uno strato adsorbito di ioni solvatati (strato di Stern);

c) uno strato diffuso di ioni e molecole orientate (strato di GouyChapman)

Per definizione il potenziale elettrico è il lavoro necessario per portare una carica da distanza infinita (bulk della soluzione) nell’interno del metallo. La ddp (differenza di potenziale) invece è la variazione di lavoro da un punto all’altro. Tuttavia essendo le soluzioni elettrolitiche più complicate rispetto al metallo in soluzione, il potenziale elettrico non può essere considerato da solo, così come accade anche al potenziale chimico, perché questi sistemi sperimentano sia fenomeni chimici che fenomeni elettrici. A questo scopo Guggenheim introdusse il concetto di potenziale elettrochimico:

μ_el= μ + + z N_{A x} e Φ

pot elettrochimico = potenziale chimico + potenziale elettrico

I metalli in generale sono ottimi conduttori di corrente e secondo il modello a bande in un metallo distinguiamo dei livelli di energia occupati da elettroni e la sovrapposizione dei livelli di ogni singolo atomo porta alla formazione di gruppi di livelli o bande e nel metallo distinguiamo in particolare la banda in cui si trovano gli elettroni più esterni e una banda di energia superiore, vuota, che chiamiamo rispettivamente banda di valenza e banda di conduzione.

le bande si formano per sovrapposizione degli orbitali atomici dei singoli atomi. Per esempio se supponiamo vi siano 3 atomi di metallo, gli orbitali 1S formano una banda 1s costituita da 3 orbitali 1s ognuno proveniente da un singolo atomo e sovrapposti l’un l’altro.. Se gli atomi sono n si formerà una banda 1s costituita da n orbitali, simili bande si formano con gli altri orbitali. In questo modello a bande gli elettroni di valenza occupano orbitali che sono delocalizzati su tutto il solido. Se immaginiamo un solido unidimensionale per esempio considerando gli atomi uno accanto all’altro lungo l’asse X quindi con allineamento infinito di atomi ciascuno con un orbitale s disponibile per formare orbitali molecolari, si osserva che aggiungendo N atomi si otterranno N orbitali che copriranno una banda di energie di larghezza finita.

Gli elettroni in un solido allo stato elementare ed alla temperatura di 0 gradi K , che obbediscono al Principio di Pauli che vieta loro di potersi trovare nello stesso livello di energia (orbitale) con tutti i numeri quantici uguali, riempiono gli stati elettronici loro consentiti partendo dal livello energetico più basso via via più in su, fino a che tutti gli elettroni del solido abbiano occupato i livelli di energia consentiti e si distribuiscono nei livelli di energia del solido secondo una distribuzione statistica detta di Fermi-Dirac ed il livello energetico più alto occupato dagli elettroni si chiama livello di Fermi. Nel caso in cui vi sia una banda, fra le ultime riempite da elettroni, che è parzialmente riempita e restano degli stati vuoti siamo in presenza di un metallo in cui gli ultimi elettroni hanno la possibilità di spostarsi in livelli energetici molto vicini, infinitesimalmente più alti in energia, e dunque hanno la possibilità di una mobilità elevata che porta il sistema ad essere un buon conduttore di elettricità. Nel caso in cui l’ultima banda è stata riempita completamente in modo tale che il prossimo stato elettronico consentito si trovi sulla banda successiva e fra questa banda e la banda completamente riempita c’è un Gap di energia siamo in presenza di un isolante. Nei semiconduttori invece il gap di energia tra banda di valenza e banda di conduzione è talmente piccolo che a temperatura ambiente c’è una certa probabilità che gli elettroni si trovino a saltare il gap di energia per agitazione termica, e dunque il sistema si trovi in una situazione prossima a quella di un metallo per cui può condurre la corrente.

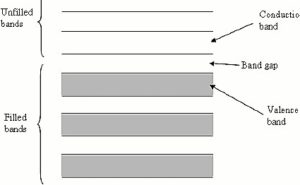
Gli elettroni di valenza infatti non risultano legati ad un tipo di ione ma al reticolo nel suo complesso. Possiamo spiegare queste proprietà osservando che gli atomi di molti elementi che formano legami metallici hanno un’energia di ionizzazione bassa. Un valore basso dell’energia di ionizzazione significa che un atomo lega debolmente gli elettroni di valenza. Di conseguenza nel solido, gli elettroni di valenza si separano facilmente dai loro atomi ed assumono una distribuzione abbastanza uniforme di carica negativa : in altri termini si viene a creare un “gas di elettroni”.

Per ogni conduttore esiste il livello di energia di Fermi che rappresenta la differenza di energia tra i livelli HOMO e LUMO (HOMO cioè highest occupied molecular orbital, orbitale molecolare a più alta energia occupato e LUMO cioè lowest unoccupied molecular orbital, orbitale molecolare a più bassa energia non occupato). Quando due metalli vengono messi a contatto si avrà conduzione fino al raggiungimento dell’equilibrio, che si verifica quando i livelli di Fermi dei due conduttori si eguagliano.

Anche nelle soluzioni elettrolitiche esiste un Livello di Fermi che corrisponde ai livelli energetici più alti per la specie che si riduce (banda di conduzione) mentre nelle specie ossidate il livello di fermi si trova nella banda di valenza in quanto accettano elettroni.

Il livello di Fermi rappresenta la separazione tra il potenziale in soluzione ed il potenziale dell’elettrodo metallico.

Il lavoro che porta la carica da distanza infinita al centro (bulk) del metallo è il risultato della combinazione di più lavori:

∞ →superficie dell’elettrodo POTENZIALE DI VOLTA
attraversamento della superficie POTENZIALE DI SUPERFICIE
∞ → interno metallo POTENZIALE GALVANI (o INTERNO)

il potenziale di superficie è costituito dal contributo degli ioni presenti all’interfase liquido-metallo e dal contributo dei dipoli orientati inquesta regione.

I potenziali tipici di un elettrodo metallico sono:

POTENZIALE DI VOLTA
POTENZIALE GALVANI

POTENZIALE DI VOLTA

nelle due parti dell’interfaccia metallo soluzione si crea una differenza di potenziale di cui una parte è costituita dal potenziale di Volta dovuto proprio alla presenza delle cariche nelle due facce.

POTENZIALE GALVANI O INNER POTENTIAL

la differenza di potenziale dovuta al lavoro fatto per portare una carica unitaria dall’infinito nel vuoto al centro del metallo.

In conclusione il Potenziale di un elettrodo che indichiamo con E è il risultato del contributo dei potenziali volta e galvani da cui si può dedurre che è impossibile misurare il valore assoluto di E, però, possiamo misurare un valore di E relativo ad un elettrodo preso come riferimento ed a cui si attribuisce per convenzione il valore E=0: tale elettrodo di riferimento è l’elettrodo ad idrogeno.

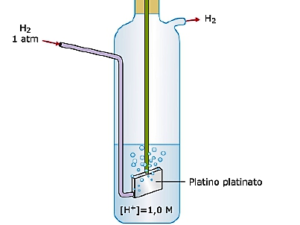
come si vede in figura, l’elettrodo di riferimento è costituito da una lamina di platino rivestita da uno strato poroso di polvere di platino che è contenuta in una capsula di vetro immersa in una soluzione 1 M di HCl ed attraverso cui si fa gorgogliare idrogeno gassoso alla pressione di 1 atmosfera.L’ elettrodo viene usato alla temperatura di 25°C .La reazione che si verifica sulla superficie del platino nell’elettrodo ad idrogeno è la seguente

2H+ (acq) ⇄ H2(g)

L’ elettrodo ad idrogeno, per essere utilizzato come riferimento, deve essere collegato con l’elettrodo di cui si vuol calcolare il valore di E relativo, cioè occorre creare un circuito elettrico costituito dall’elettrodo metallico e dall’elettrodo ad idrogeno collegati attraverso un ponte salino.La figura seguente mostra un esempio di cella elettrochimica, costituita da un elettrodo di Zinco ed un elettrodo ad idrogeno in cui il ponte salino è un tubicino contenente KNO3 in soluzione ed alle cui estremità vi sono due setti porosi( questo permette la continuità elettrica tra i due elettrodi ma non passaggio di sostanza).

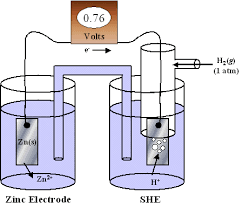
I due elettrodi sono collegati ad un volmetro che misura la differenza di potenziale tra i due elettrodi che vengono anche chiamati semicelle. Abbiamo quindi un circuito elettrico costituito da due semicelle una delle quali è la semicella ad idrogeno e l’altra una semicella del metallo.

Il circuito che vediamo in figura viene rappresentato con la seguente convenzione :

La semicella in cui si ha ossidazione (un elemento che cede elettroni si dice che si ossida mentre un elemento che acquista elettroni si dice che si riduce) costituisce l’anodo e si scrive a sinistra e quella in cui si ha riduzione(catodo) a destra.

Possiamo osservare che una cella elettrochimica o galvanica è un dispositivo che è in grado di trasformare l’energia di una reazione chimica in energia elettrica .Infatti,gli elettroni che rimangono sulla lamina metallica si muovono attraverso il filo elettrico che lo collega sia al volmetro che all’altro elettrodo che diviene fonte di elettroni ed al quale si avvicinano attratte gli ioni positivi come l’ H+ che forma quindi H2 (ricordiamo che la corrente elettrica si muove in senso inverso a quello degli elettroni). Vedremo in seguito che è possibile anche far avvenire una reazione non spontanea utilizzando l’energia elettrica che viene quindi trasformata in energia chimica ( in tal caso si ha una cella elettrolitica in cui avviene cioè l’elettrolisi).

ALTRI TIPI DI ELETTRODI DI RIFERIMENTO

Dal momento che nella comune pratica di laboratorio l’uso dell’elettrodo ad idrogeno è complicato dal fatto che occorre avere una sorgente di idrogeno(bombola) ed essendo l’idrogeno un gas che presenta problemi di sicurezza, sono stati messi a punto altri elettrodi di riferimento che non utilizzano l’idrogeno ma che possiedono un valore di potenziale costante ad una data temperatura e possono essere usati in condizioni diverse.Un elettrodo di riferimento deve possedere un potenziale noto e costante, indipendente dalla composizione della soluzione da misurare.

ELETTRODO A CALOMELANO

Questo elettrodo utilizza il calomelano che è il cloruro di mercurio (I)Hg2Cl2.

L’elettrodo a calomelano saturo (SCE) consiste in un filo di platino immerso in mercurio liquido, a sua volta a contatto con una pasta di mercurio liquido, calomelano (Hg2Cl2) e KCl immersa in una soluzione satura di KCl ed Hg2Cl2.

La reazione che si osserva nell’elettrodo(semicella) Hg/Hg2Cl2/KCl è:

Hg2Cl2 + 2 e ⇄ 2Hg + 2 Cl-

il cui potenziale è :

E= E° – 0,0591/2 log [Cl-]² cioè

E= E° – 0,0591 log [Cl-]

o meglio E= E° – 0,0591 log [Cl-] x f

dove f = coeff.di attività e [Cl-] x f=attività Cl-

ed essendo E°= 0,2682 V

E=0,2682 -0,0591 log a_Cl-

Il potenziale dipende dall’attività di Cl- nella soluzione a contatto con Hg2Cl2. Nell’elettrodo si usa KCl 3M per evitare la formaione di cristalli di KCl sul fondo dell’eletrodo che possono otturare il setto poroso. Sono anche usati elettrodi con KCl 0,1 ed 1 M. questo elettrodo può essere usato fino a temperature di +70°C perchè a temperature superiori il calomelano subisce una dismutazione spontanea cioè il mercurio Hg+ forma sia Hg° che Hg+2.I solfuri,gli ossidanti ed i forti riducenti lo danneggiano così come isostanze complessanti in grado di formare amalgami col mercurio Hg+2.Tutto ciò si evita ricorrendo ad un setto poroso contenente un elettrolita intermedio si ha così un elettrodo a doppia giunzione.Il potenziale dell’elettrodo a calomelano saturo è pari a +0,241V rispetto all’elettrodo standard ad idrogeno.

ELETTRODO DI RIFERIMENTO ARGENTO/CLORURO DI ARGENTO

L’elettrodo ad argento/cloruro d’argento è costituito da un elettrodo di argento rivestito di AgCl ed immerso in una soluzione acquosa satura di KCl e AgCl.

Nella semicella Ag/AgCl/KCl(aq) la reazione che si verifica è :

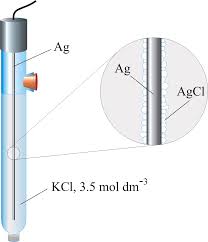
AgCl +e ⇄ Ag° + Cl-

ed il suo potenziale è dato dalla E=E° – 0,0591 log[Cl-]x f

E°= 0,2389 V a 25° quando KCl=1M pertxanto:

E= 0,2389- 0,0591 log a_Cl-

Il potenziale di un elettrodo ad argento/cloruro d’argento contenente una soluzione satura di KCl è pari a +0,197 V rispetto all’elettrodo standard ad idrogeno.

COME CALCOLARE IL POTENZIALE DI UNA CELLA GALVANICA

Il potenziale di un elettrodo può essere misurato sperimentalmente utilizzando la cella galvanica in cui uno degli elettrodi è l’elettrodo ad idrogeno (o un altro elettrodo di riferimento).

Infatti, se consideriamo le reazioni che avvengono ai due elettrodi vediamo che :

Mⁿ⁺ + ne-⇄ M

2H⁺ ⇄ H2 + ne

quindi nella cella si ha l’equilibrio:

Mⁿ⁺ + H2⇄ M + 2H⁺

sappiamo, inoltre, che all’interfaccia metallo-soluzione vi è una variazione di energia libera

ΔG = Gsol -Gmet

e questa dipende dal numero di cariche che passano in soluzione e dalla corrente che questo passaggio determina, ed infine, dipende dal potenziale dell’elettrodo E:

se l’elettrodo si trova in uno stato standard (25°C ed 1 atm)

ΔG° = – ne F E°

tuttavia, sappiamo che l’equilibrio sopra descritto determina una variazione di energia libera ΔG pari a

ΔG=ΔG⁰ +RTln Keq

da cui si ha ΔG=-ne FE° +RTln Keq si deduce perciò che

– nFe E = -nFeE° + RT ln Keq da cui

E= E° – RT/nFe ln K

ma K = 1/[M+n] pertanto E=E° -RT/nFe ln 1/[M⁺ⁿ]

e passando dai logaritmi naturali a quelli decimali e ricordando che il Log 1/x = Log 1 – logx e che log1 =0

E=E° -RT/nFe (log1 – log[M⁺ⁿ] )

usando il valore di [M⁺ⁿ] = 1 M si ha che il potenziale misurato sul volmetro della cella galvanica E non è altro che il valore del potenziale standard dell’elettrodo metallico E° infatti poichè

-RT/nFe x ln 1 =0

E=E°

Con questo metodo sono stati misurati i valori di E° per tutti i metalli ed è stata creata una scala di valori al cui centro vi è il potenziale dell’idrogeno per convenzione uguale a zero. L’altra convenzione utilizzata è che sono stati considerati e tabulati i valori di E° relativi alle riduzioni non alle ossidazioni per esempio la reazione considerata è :

M+n +ne ⇄ M

il cui E° misurato è E° di riduzione.

Ovviamente se si considera la reazione di ossidazione

M ⇄ M+n +ne

il valore di E° deve cambiare di segno cioè E° _riduz.= – E° _ossid

Valori tabulati dei potenziali standard

Nella tabella seguente vengono indicati i valori dei potenziali di riduzione standard misurati :

Catodo	Potenziale di riduzione standard E⁰ (volt)
3N₂ + 2H⁺ + 2e⁻ → 2HN₃	−3,09
Li⁺(aq) + e⁻ → Li(s)	−3,04
Rb⁺ + e⁻ → Rb(s)	−2,98
K⁺(aq) + e⁻ → K(s)	−2,93
Cs⁺(aq) + e⁻ → Cs(s)	−2,92
Ba²⁺(aq) + 2e⁻ → Ba(s)	−2,91
Sr²⁺(aq) + 2e⁻ → Sr(s)	−2,89
Ca²⁺(aq) + 2e⁻ → Ca(s)	−2,76
Na⁺(aq) + e⁻ → Na(s)	−2,71
Mg(OH)₂ + 2e⁻ → Mg + 2OH⁻	−2,69
Mg²⁺(aq) + 2e⁻ → Mg(s)	−2,38
H₂AlO₃⁻(aq) + H₂O + 3e⁻ → Al(s) + 4OH⁻	−2,35
N₂(g) + 2H₂O + 4H⁺ + 2e⁻ → 2NH₃OH⁺(aq)	−1,87
Al³⁺(aq) + 3e⁻ → Al(s)	−1,66
HPO₃²⁻(aq) + 2H₂O + 2e⁻ → H₂PO₂⁻(aq) + 3OH⁻	−1,65
ZnO₂²⁻(aq) + 2H₂O + 2e⁻ → Zn(s) + 4OH⁻	−1,22
CrO₂⁻(aq) + 2H₂O + 3e⁻ → Cr(s) + 4OH⁻	−1,20
Mn²⁺(aq) + 2e⁻ → Mn(s)	−1,19
2SO₃⁼(aq) + 2H₂O + 2e⁻ → S₂O₄⁼(aq) + 4OH⁻	−1,12
PO₄³⁻(aq) + 2H₂O + 2e⁻ → HPO₃²⁻(aq) + 2OH⁻	−1,05
Sn(OH)₆²⁻(aq) + 2e⁻ → HSnO₂⁻(aq) + 3OH⁻ + H₂O	−0,93
SO₄²⁻(aq) + H₂O + 2e⁻ → SO₃²⁻(aq) + 2OH⁻	−0,93
Cr²⁺(aq) + 2e⁻ → Cr(s)	−0,91
Ti³⁺(aq) + e⁻ → Ti²⁺(aq)	−0,90
TiO₂(s) + 4H⁺ + 4e⁻ → Ti(s) + 2H₂O	−0,86
2H₂O(l) + 2e⁻ → H₂(g) + 2OH⁻(aq)	−0,828
Zn²⁺(aq) + 2e⁻ → Zn(s)	−0,762
Cr³⁺(aq) + 3e⁻ → Cr(s)	−0,74
AsO₄³⁻(aq) + 2H₂O + 2e⁻ → AsO₂⁻(aq) + 4OH⁻	−0,71
PbO(s) + H₂O + 2e⁻ → Pb(s) + 2OH⁻	−0,576
Fe(OH)₃(s) + e− → Fe(OH)₂(s) + OH⁻	−0,56
2CO₂(g) + 2H⁺ + 2e⁻ → H₂C₂O₄(s)	−0,49
S(s) + H₂O + 2e⁻ → HS⁻(l) + OH⁻	−0,48
S(s) + 2e⁻ → S²⁻(aq)	−0,476
Fe²⁺(aq) + 2e⁻ → Fe(s)	−0,41
Cd²⁺(aq) + 2e⁻ → Cd(s)	−0,40
Co²⁺(aq) + 2e⁻ → Co(s)	−0,28
Ni²⁺(aq) + 2e⁻ → Ni(s)	−0,257
Sn²⁺(aq) + 2e− → Sn(s)	−0,14
Pb²⁺(aq) + 2e⁻ → Pb(s)	−0,13
Fe³⁺(aq) + 3e⁻ → Fe(s)	−0,04
2H⁺(aq) + 2e⁻ → H₂(g)	0,00
Sn⁴⁺(aq) + 2e⁻ → Sn²⁺(aq)	0,15
Cu²⁺(aq) + e⁻ → Cu⁺(aq)	0,16
ClO₄⁻(aq) + H₂O(l) + 2e− → ClO₃⁻(aq) + 2OH⁻(aq)	0,17
S₄O₆²⁻(aq) + 2e⁻ → 2S₂O₃²⁻(aq)	0,2
AgCl(s) + e⁻ → Ag(s) + Cl⁻(aq)	0,22
Cu²⁺(aq) + 2e⁻ → Cu(s)	0,34
ClO₃⁻(aq) + H₂O(l) + 2e⁻ → ClO₂⁻(aq) + 2OH⁻(aq)	0,35
IO⁻(aq) + H₂O(l) + 2e⁻ → I⁻(aq) + 2OH⁻(aq)	0,49
Cu⁺(aq) + e⁻ → Cu(s)	0,52
I₂(s) + 2e⁻ → 2I⁻(aq)	0,54
ClO₂⁻(aq) + H₂O(l) + 2e⁻ → ClO⁻(aq) + 2OH⁻(aq)	0,59
Fe³⁺(aq) + e⁻ → Fe²⁺(aq)	0,77
Hg₂²⁺(aq) + 2e⁻ → 2Hg(l)	0,80
Ag⁺(aq) + e⁻ → Ag(s)	0,80
Hg²⁺(aq) + 2e⁻ → Hg(l)	0,85
ClO⁻(aq) + H₂O(l) + 2e⁻ → Cl⁻(aq) + 2OH⁻(aq)	0,90
2Hg²⁺(aq) + 2e⁻ → Hg₂²⁺(aq)	0,90
NO₃⁻(aq) + 4H⁺(aq) + 3e⁻ → NO(g) + 2H₂O(l)	0,96
Br₂(l) + 2e⁻ → 2Br⁻(aq)	1,07
O₂(g) + 4H⁺(aq) + 4e⁻ → 2H₂O(l)	1,23
Cr₂O₇²⁻(aq) + 14H⁺(aq) + 6e⁻ → 2Cr³⁺(aq) + 7H₂O(l)	1,33
Cl₂(g) + 2e⁻ → 2Cl⁻(aq)	1,36
Ce⁴⁺(aq) + e⁻ → Ce³⁺(aq)	1,44
MnO₄⁻(aq) + 8H⁺(aq) + 5e⁻ → Mn²⁺(aq) + 4H₂O(l)	1,49
H₂O₂(aq) + 2H⁺(aq) + 2e⁻ → 2H₂O(l)	1,78
Co³⁺(aq) + e⁻ → Co²⁺(aq)	1,82
S₂O₈²⁻(aq) + 2e⁻ → 2SO₄²⁻(aq)	2,01
O₃(g) + 2H⁺(aq) + 2e⁻ → O₂(g) + H₂O(l)	2,07
F₂(g) + 2e⁻ → 2F⁻(aq)	2,87

COME POSSIAMO UTILIZZARE I POTENZIALI DI RIDUZIONE STANDARD?

PROCEDIAMO CON UN ESEMPIO:

si consideri una lamina di Zn immersa in una soluzione contenente ioni Cu⁺²: cosa avviene?

sperimentalmente si osserva che lo zinco si ossida passando in soluzione ed il rame si riduce depositandosi sulla lamina di zn.

E’ possibile prevedere questo comportamento se valutiamo i rispettivi E°:

Cu⁺²(aq) + 2 e → Cu E°= + 0, 34 Volts

Zn²⁺(aq) + 2e⁻ → Zn(s) E°= – 0,762 Volts

dobbiamo ricordare che:

Gli elementi con E° PIÙ POSITIVO (o meno negativo) agiscono da OSSIDANTI nei confronti di elementi con E° meno positivo (o più negativo)

Infatti il fluoro che ha un E° di 2,87 V ha un fortissimo potere ossidante.

Gli elementi con E° MENO POSITIVO O NEGATIVO agiscono da RIDUCENTI nei confronti di elementi con E° più positivo (o meno negativi)

Il rame ha un E° è più positivo dello Zn quindi agisce da ossidante nei suoi confronti.

Lo Zn che ha E° negativo ha maggiore tendenza ad agire da riducente nei confronti del rame

SECONDO ESEMPIO

COSA SUCCEDE SE PONIAMO UNA LAMINA DI Cu IN UNA SOLUZIONE DI Zn⁺²?

in relazione ai potenziali E° lo Zn dovrebbe agire da riducente ossidandosi, ma il Rame è allo stato metallico e quindi non può ridursi ulteriormente, e lo zinco è già ossidato, pertanto, sperimentalmente non si osserva alcun cambiamento.

ALTRO ESEMPIO

PUO’ VERIFICARSI QUESTA REAZIONE IN MODO SPONTANEO?

Fe + Cu2+ → Fe2+ + Cu

le reazioni che dovrebbero avvenire sono :

l’ossidazione del Ferro Fe→Fe+2 + 2e
la riduzione del rame Cu+2 + 2 e → Cu

i potenziali di riduzione standard sono :

Fe²⁺(aq) + 2e⁻ → Fe(s) E°_{Fe = – 0,04 V}

LA REAZIONE DI CUI SOPRA

Fe→Fe+2 + 2e E°= +0,04 V

Cu+2 + 2 e → Cu E°_{Cu = +0,34 V}

da quanto esposto sopra, il rame agisce da ossidante quindi a contatto col Fe metallico lo ossida a Fe+2 pertanto la reazione

Fe + Cu2+ → Fe+2 + Cu

avviene in modo spontaneo.

ANCORA UN ESEMPIO

QUALE TRA QUESTI ELEMENTI REAGISCE SE PONIAMO IN UNA SOLUZIONE

Cu+2 Zn+2 Fe Ni

per rispondere a questa domanda ricorriamo ai valori di E°

Cu⁺²(aq) + 2 e → Cu E°_{Cu = +0,34 V}

Fe²⁺(aq) + 2 e⁻ → Fe(s) E°_{Fe = – 0,04 V}

Ni²⁺(aq) + 2 e⁻ → Ni(s) E°_Ni= -0,257 V

Zn²⁺(aq) + 2e⁻ → Zn(s) E°_Zn= – 0,762 V

da questi dati si vede che il rame Cu+2 agisce da ossidante nei confronti di tutti e tre gli elementi, tuttavia lo Zn è già ossidato ma sia Fe che Ni reagiscono. Quale dei due reagisce prima? dai valori di E° si vede che il primo ad essere ossidato è il Ferro Fe che ha un E° meno negativo del Ni quindi, quando tutto il ferro sarà stato ossidato inizierà ad ossidarsi il Ni. Il rame formerà rame metallico in quanto si riduce.