CONCETTO DI GRUPPO

In linea generale, possiamo definire un “gruppo” co­me un insieme di elementi fra di loro in relazione mediante alcune regole ben determinate. Quindi, affinché un certo numero di elementi formi un gruppo, è necessario che  obbediscano alle regole seguenti:
1)-Il prodotto fra due elementi del gruppo deve essere un altro elemento appartenente allo stesso gruppo. Occorre, però, precisare che, il prodotto o moltiplicazione fra due o più elementi del gruppo non è necessariamente di ti­po aritmetico, ma intendiamo qui per moltiplicazione il susseguirsi di due operazioni. Ad Es. fra i gruppi che noi considereremo, vi sono i gruppi di simmetria i cui elementi possono dare origine ad operazioni ad esempio: assi, piani , centri di una determinata struttura geometrica sono elementi di simmetria con i quali possiamo compiere dei movimenti quali ad es. rotazioni intorno agli assi, riflessioni sui piani oppure inversioni. Questi movimenti rappresentano gli elementi del gruppo. Se li definiamo con delle lettere avremo gli elementi di gruppo P, Q, R, S.  Dire che Q moltiplica P significa che sulla figura  si esegue prima il movimento Q poi quello P.

QP= R

Questi movimenti contigui, porteranno la figura su cui operiamo ad una posizione che può essere raggiunta anziché con i due movimenti precedenti, con un solo movimento diverso dai primi due e cioè ad es. R. Quest’ultimo movimento deve essere un elemento del gruppo a cui appartenevano i primi due.

Riassumendo, possiamo  scrivere il prodotto di due elementi del gruppo con la notazione:    QP=R

Con ciò indichiamo che la prima operazione è quella Q a cui segue l’operazione P ed il risultato l’operazione R.
Risulta evidente che l’operazione Q seguita da quella P può non dare lo stesso risultato che si otterrebbe compiendo prima l’operazione P e poi quella Q. Cioè, mentre è noto dall’aritmetica che scrivere 7 x 5 oppure  5 x 7 è perfettamente la stessa perchè si ottiene sempre lo stesso risultato,  nel caso  degli elementi di simmetria la moltiplicazione AB può non dare le lo stesso risultato di BA.
Esiste, tuttavia,qualche gruppo i cui elementi commutano, cioè, godono della proprietà QP =PQ : in questo caso il gruppo a cui appartengono questi elementi di simmetria viene detto Abeliano.

2-La seconda regola è che  deve essere valida la proprietà associativa cioè:

(P Q) R = P (Q R)

In definitiva, possiamo compiere prima la moltiplicazione tra R e Q ( tra parentesi) nell’ordine da destra a sinistra, ed otterremo ad esempio come risultato l’elemento Z, se poi moltiplichiamo quest’ultimo per P, otterremo come risultato l’elemento Y.
Tuttavia possiamo ugualmente ottenere come risultato delle operazioni di moltiplicazione fra R e ( P Q ) il prodotto Y. Se tutto ciò avviene, gli elementi suddetti possono appartenere ad un gruppo.

3)— Fra gli elementi del gruppo deve esservene almeno uno che moltiplicato per qualunque altro elemento del gruppo  deve necessariamente commutare; cioè deve essere:

E P = PE =

tale elemento viene definito identità, e si indica con E
4) Ogni elemento del gruppo, deve avere un reciproco, cioè se P è un elemento, deve esistere il reciproco 1/P = P ^{– 1} Il quale è un altro elemento dello stesso gruppo.
Possiamo notare che P^-1 è il reciproco di P, se P^-1 P = P P-1 = E    dove E indica l’elemento identità.

Possiamo anche definire un teorema riguardante il reciproco di un prodotto di due o più elementi.

Il reciproco di un prodotto di due o più elementi uguale al prodotto dei reciproci.

ad es. siano gli elementi P Q R S consideriamo il prodotto (PQRS) ed anche il suo reciproco cioè ( PQRS )^-1, diremo allora
che: ( PQRS)^{-1  =}  S^-1  R^-1  Q^-1  P^-1
Per provare quanto asserito sopra diciamo che il prodotto PQRS è l’elemento D del gruppo stesso a cui appartengono PQRS, quindi scriviamo:
PQRSD=D
moltiplicando il membro di destra e quello di sinistra per S^-1  R^-1  Q^-1  P^-1  si  ottiene 

(PQRS)  (S^-1  R^-1  Q^-1  P^-1  )  = D S^-1  R^-1  Q^-1  P^-1
ma ricordiamo che X ^-1X = E,    per cui      E = S^-1  R^-1  Q^-1  P^-1  

in base a ciò è evidente che affinchè questo sia possibile è necessario che  S^-1  R^-1  Q^-1  P^-1  = D^-1

pertanto essendo D = PQRS   allora D^-1 = S^-1  R^-1  Q^-1  P^-1  

ELEMENTI ED OPERAZIONI DI SIMMETRIA

Gli elementi di simmetria sono entità geometriche quali PIANI,ASSI,CENTRI  sui quali possiamo compiere alcun operazioni quali riflessione sui piani rotazione intorno agli assi ecc.

L’esistenza degli elementi è quindi dimostrata in quanto possiamo eseguire operazioni su di loro.

Le rotazioni, riflessioni, inversioni sono tali che dopo averle eseguite, la figura geometrica su cui operiamo si ritroverà in una posizione equivalente a quella originaria.

Le operazioni di simmetria che possiamo utilizzare sono descritte nello specchietto seguente.

___________________________________________________________________________________

ELEMENTO DI SIMMETRIA                                                                            OPERAZIONI  CORRISPONDENTI

___________________________________________________________________________________

PIANO                                                                                                                                RIFLESSIONI SUL PIANO

CENTRO DI SIMMETRIA

O CENTRO DI INVERSIONE                                                                                       INVERSIONI ATTORNO AL CENTRO

ASSE PROPRIO                                                                                                               UNA O PIU’ ROTAZIONI INTORNO ALL’ASSE

ASSE IMPROPRIO                                                                                                          ROTAZIONE SEGUITA DA RIFLESSIONE

SU PIANO PERPENDICOLARE ALL’ASSE DI

ROTAZIONE

PIANO DI SIMMETRIA E RIFLESSIONE SUL PIANO

E’ necessario che il piano di simmetria attraverSi il corpo considerato ( nel Nostro caso, come vedremo, il corpo è rappresentato dalla molecola). Per vedere se il piano preso in considerazione è un piano di simmetria, è importante osservare se le operazioni (su di esso portano il corpo ad assumere una configurazione equivalente a quella che esso possedeva prima dell’operazione. Per provare ciò, natural­mente, ci riferiamo ad un sistema di assi cartesiani :

supponiamo adesso di avere una molecola formata da 3 atomi di cui due che giacciono sul piano xy ed una sul piano xz

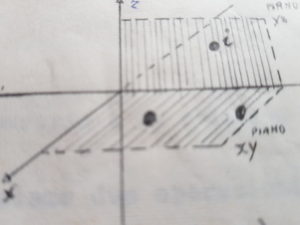
abbiamo chiamato i l’atomo che sta sul piano xz perpendicolare a xy .

Operiamo adesso su questa molecola una operazione di RIFLESSIONE rispetto al piano xy : otteniamo

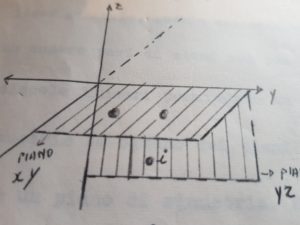
la figura ottenuta è equivalente a quella iniziale infatti le coordinate sul piano xy rimangono uguali e varia solo la coordinata z dell’atomo i . Possiamo dire che il piano xy su cui abbiamo effettuato l’operazione di riflessione è un piano di simmetria. I piani di simmetria si indicano con la lettera greca sigma σ.

Possiamo anche notare che se effettuiamo ancora una riflessione successiva otteniamo la figura di partenza per cui possiamo scrivere che 

σσ =E cioè si ottiene l’operazione identità . Se anziché effettuare due riflessioni avessimo effettuato direttamente l’operazione identità E, avremmo ottenuto lo stesso risultato ottenuto con le due riflessioni. 

APPLICHIAMO IL CONCETTO DI PIANO DI SIMMETRIA ALLE MOLECOLE 

se si applicano n riflessioni successive si avrà σⁿ= E nel caso in cui n è un numero pari, mentre e il σⁿ= o se n è un numero dispari. In linea generale, quelle molecole non planari che possiedono un numero pari di atomi non possiedono piani di simmetria. Te molecole lineari possiedono un numero infinito di piani simmetria ed ognuno dei piani che contiene l’asse molecolare è un piano di simmetria. Fra questi due casi estremi, naturalmente, esistono molte altre molecole che possiedono un numero limitato di piani. Prendiamo ad es. la molecola di H2 O e supponiamo giaccia su un piano XY :

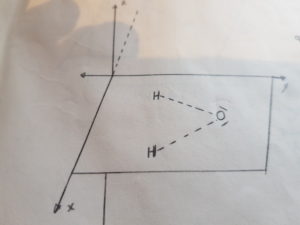
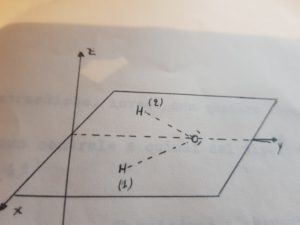
Un piano di simmetria è quello in cui giace la molecola, l’altro è invece quello verticale che divide la molecola in due e che contiene l’atomo di ossigeno, cd è perpendicolare al primo. Compiendo una riflessione su questo piano verticale (la indichiamo con σv),cambiano di posizione solo i due atomi di H , mentre l’atomo di ossigeno rimane dove si trovava prima della riflessione. Ad es. se ci riferiamo ad un sistema  di assi cartesiani, ogni atomo sarà caratterizzato da tre coordinate: l’atomo di idrogeno avrà le coordinate -X₁Y₁ O   il secondo atomo di idrogeno avrà le coordinate X₂Y₂O l’atomo di ossigeno avrà le coordinate X₃Y₃O.

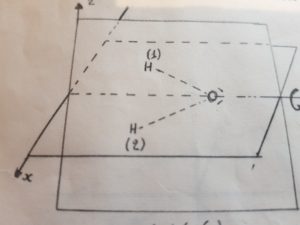
Se adesso effettuiamo una riflessione allora l’idrogeno H 1 con  le coordinate -X1Y1O dopo l’operazione avrà coordinate X1Y1O il secondo atomo di idrogeno H 2 che aveva le coordinate X2Y2O avrà dopo l’operazione le coordinate   -X2Y2O, mentre l’ossigeno non muterà le sue coordinate. In definitiva si otterrà la figura seguente:

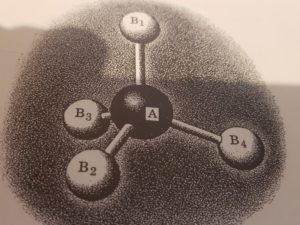
MOLECOLE TETRAEDRICHE    AX4

Le molecole tetraedriche con quattro atomi diversi tra loro legati all’atomo centrale hanno i seguenti piani di simmetria:

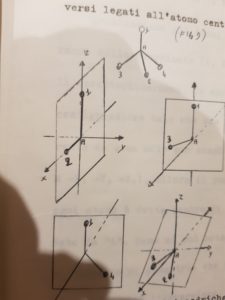
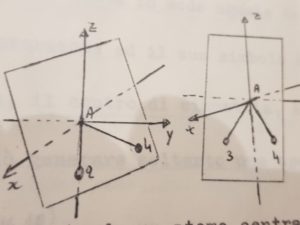
I PIANI CHE ABBIAMO INDICATO SOPRA SONO :

AB1B2      AB1B3     AB1B4

AB2B3      AB2B4   AB3B4

CENTRI DI INVERSIONE

Consideriamo gli atomi di una molecola; essi possederanno delle coordinate X,Y,Z  che  li caratterizzano. Se sarà possibile ottenere una nuova configurazione tale che sia equivalente alla a prima e differente da essa solo per scambio delle coordinate (da X,Y,Z  alle nuove coordinate —X, —Y, —Z,), allora il punto che dista in modo uguale da ogni atomo è detto centro di inversione ed il suo simbolo è dato da “i”. Come si può notare, il centro di simmetria, è un elemento di simmetria che può generare soltanto una operazione, e cioè l’inversione. Per esempio nella molecola con struttura planare quadrata ad esempio il centro di inversione è rappresentato dall’atomo e.

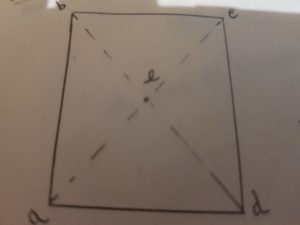
Risulta evidente che nel centro può trovarsi soltanto un atomo. Perciò, se in una molecola è presente un atomo al centro di essa, questo atomo sarà l’unico a non modificare le proprie coordinate dopo l’operazione di inversione. Se l’inversione viene eseguita più volte intorno al centro, si indicherà ciò con il simbolo iⁿ.
Si può pertanto notare che, se il numero di volte è pari, cioè se n = 2,4,6 ecc, allora iⁿ= E; se invece n è dispari cioè n=1,3,5…allora  iⁿ= j•
Esempi di molecole che posseggono centro di inversione sono molecole del tipo AB6 ottaedriche, del tipo AB4 planari e molecole trans , molecole AB2C2 planari, l’etilene ,il benzene.

ASSI E ROTAZIONI PROPRIE

Un asse di rotazione è una retta immaginaria perpendicolare ad un piano  ed attraversa la molecola. Il simbolo di un asse di simmetria è Cn dove n è l’ordine dell’asse intendendo per ordine il numero di volte che occorre ruotare la molecola intorno all’assa per ottenere una configurazione equivalente all’iniziale.

Se consideriamo una molecola trigonale planare  come ad esempio il ciclopropano 

 possiamo notare che vi può essere un asse di simmetria che permette una configurazione equivalente a quella iniziale C3,perpendicolare al piano su cui giace il triangolo, infatti n=3.  In generale una rotazione intorno all’asse Cn si indica con C _n^m  in cui m indica una rotazione di m volte 2π/3 .

Si deduce che l’operazione riflessione su un piano è unica per ogni piano, così come l’operazione inversione è unica rispetto ad un centro di inversione, nel caso di un asse di simmetria vi possono essere n operazioni 

Cn, Cn¹,Cn²…….Cnⁿ =E

Per una molecola trigonale planare vi sono quindi i seguenti assi : 1 asse C3 e 3 assi C2

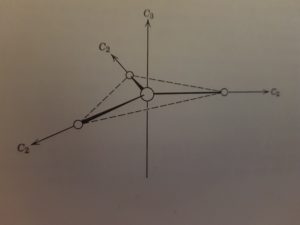
per una molecola tedraedrica si hanno i seguenti assi 

3 assi C2.

La molecola di DIFLUOROMETANO ha due piani perpendicolari tra loro  ed essendo verticali si indicano con σ_v

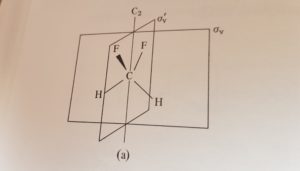
Ambedue i piani contengono l’asse C2  e siccome i piani VERTICALI contengono l’asse con valore di ordine maggiore che è C2 i piani della molecola vengono indicati con la lettera v quindi con  σ_v ed il corrispondente asse C2 è indicato come C2v.

Nel TRIFLUORURO DI BORO (BF3) esiste un solo asse C3

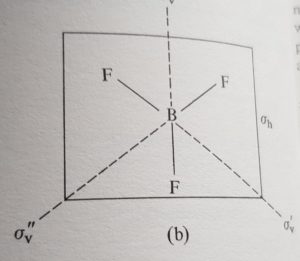
il piano su cui si trova la molecola è orizzontale e l’asse C3 è perpendicolare rispetto al piano h. In questo caso il piano orizzontale è chiamato σ_h  ed esistono inoltre 3 piani verticali che attraversano il centro della molecola: si tratta quindi di 3 piani  σv.

Nel composto ALLENE, due atomi di idrogeno giacciono sul piano orizzontale (quelli a destra in figura)  mentre gli altri due giacciono sul piano verticale, il primo biseca l’angolo dei primi due atomi di H ed il secondo biseca l’angolo degli altri due.Questi piani di simmetria vengono definiti DIAGONALI  e vengono indicati con σ_d

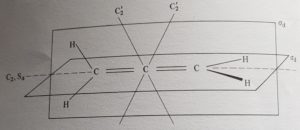
ne risulta che esiste un asse C2 che unisce gli atomi di idrogeno ma esistono anche  due assi C2 obliqui  che vengono pertanto definiti C_2d

Se consideriamo l’anilina,

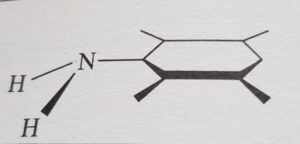
in questo caso 2 atomi di idrogeno del gruppo amminico non sono complanari come il resto della molecola per cui il piano individuato si indica con la sola lettera sigma σ.

ROTAZIONI IMPROPRIE OVVERO ROTAZIONI SEGUITE DA RIFLESSIONE SU UN PIANO

Sono rotazioni improprie le  rotazioni seguite da riflessione su un piano perpendicolare all’asse intorno al quale avviene la rotazione. L’asse viene definito asse improprio e l’operazione completa viene indicata con il simbolo Sn, il quale indica una rotazione improria di 2π/n . L’esistenza di un asse Cn perpendicolare ad un piano rende quindi possibile una rotazione impropria cioè un’operazione Sn. Tuttavia è possibile un’operazione Sn anche se non esiste un piano perpendicolare all’asse Cn.

Consideriamo la molecola di etano:

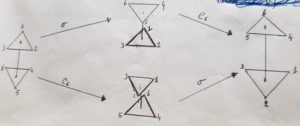
 se eseguiamo la riflessione sul piano (la freccia in alto operazione σ ) e poi eseguiamo la rotazione oraria sull’asse C  otteniamo la stessa disposizione degli atomi anche se eseguiamo prima la rotazione sull’asse e poi la riflessione. La linea che unisce i due atomi di C in realtà non definisce un asse C6 bensì un asse C3.

Le operazioni Cσ e  σC sono ambedue uguali all’operazione rotazione impropria  S6

 Anche per una molecola tetraedrica si può avere una situazione simile infatyti, il tetraedro possiede 3 assi C2 ma ognuno di essi si comporta come se fosse un asse S4 :

Se si inverte due volte la molecola cioè se si attua un’operazione  S2²   si riporta la molecola allo stato iniziale cioè  

S2² =i²  = E

in generale

     Snⁿ =EE= E

ed è come se avessimo eseguito l’operazione identità E.

OPERAZIONI DI SIMMETRIA

Prodotto o moltiplicazione tra due operazioni di simmetria significa che le operazioni vengono eseguite l’una dopo l’altra partendo da destra verso sinistra. Per esempio il prodotto AB significa che prima si esegue l’operazione B poi quella A.

Ricordiamo che il prodotto fra due elementi di un gruppo deve essere un altro elemento appartenente allo stesso gruppo.

Consideriamo un punto nello spazio caratterizzato dalle coordinate X1,Y1,Z1

compiendo su questo delle operazioni di simmetria la posizione del punto verrà modificata. Per esempio supponiamo che esistano due  assi binari  C2 e che coincidano con gli assi X ed Y.

Se effettuiamo una rotazione intorno all’asse X avremo la nuova configurazione del punto:

le coordinate del punto sono adesso X1, – Y1,-Z1 

Se eseguiamo su questa figura l’operazione C2 sull’asse Y  la nuova posizione sarà:

le coordinate saranno -X1, -Y1, +Z1 .

Pertanto il susseguirsi di due operazioni C2  su X e su Y equivale all’operazione C2 intorno all’asse Z.

Consideriamo adesso una riflessione sul piano XZ: il punto di coordinate X1,Y1,Z1 assumerà la posizione descritta dalle coordinate

X1,-Y1,Z1 

e se effettuiamo dopo la riflessione precedente anche una rotazione sull’asse Z come se si trattasse di un asse C4

pertanto le due operazioni di riflessione e rotazione σ  e C4   (C4σ ) danno luogo al risultato seguente 

C4(z) σ (X,Y) [X1,Y1,Z1] → C4(z) [X1,-Y1,Z1] → [-x1,-y1,z1]

Se consideriamo adesso un piano diagonale come in figura 

eseguiamo l’operazione di riflessione su un piano σd diagonale, cioè un piano passante tra +Y e -X : questa operazione trasforma il punto [X1,Y1,Z1] in un altro punto [-Y1,-X1,Z1]. In pratica il risultato dell’operazione σd è analogo a quello ottenuto col susseguirsi di due operazioni C4(z) σ (xz) pertanto Cn(z) σ(xz) = σd

 ROTAZIONE INTORNO AD UN ASSE ED INVERSIONE

La roto-riflessione è equivalente all’operazione S descritta sopra ma l’ordine dell’operazione non è lo stesso  e l’operazione si indica con I  . Un’0perazione in senso orario S4 è equivalente ad una operazione roto-inversione I4 per esempio nell’etano si ha :

rotazione↓

Nel caso in cui un elemento A può essere trasformato in B per azione di una operazione fra A ed un elemento X cioè ad es. AX= B se è possibile riottenere da B,  A mediante un’altra operazione con X^-1   si dirà allora che A e B sono equivalenti. Se A può essere trasformato in C, dovrà esserci  un mezzo per trasformare anche B in C; in tal caso A, B, C. formano un gruppo equivalente. Per es, sia data la molecola planare triangolare BF3 ognuno degli assi C2 giacenti sul piano possono essere mossi in modo tale da coincidere tra loro per rotazione di 2π/3  e 2 x 2π/3 . Queste in effetti sono operazioni di simmetria ed i tre assi binari vengono detti equivalenti.
Una volta stabiliti quali siano gli elementi di simmetria posseduti dalla molecola, si osservano le operazioni a cui essi possono dar luogo. Si raggruppano queste operazioni e si osserva se soddisfano tutte le condizioni necessarie a che esse formino un gruppo. E’ evidente, quindi, che possiamo classificare le molecole a seconda delle operazioni che possiamo effettuare con gli elementi di simmetria della molecola.

In relazione a quanto sopra, vediamo quali siano gli elementi di simmetria e le operazioni conseguenti per la molecola di acqua e come possiamo costruire un gruppo.

Consideriamo la molecola di H2O che supponiamo abbia una forma geometrica triangolare come in figura:

possiamo notare la presenza di un piano verticale σv   ed assi C3 : vediamo adesso quali operazioni possiamo compiere con questi elementi di simmetria. Le operazioni possibili sono:

1-l’operazione identità E,

2-rotazione intorno agli assi ternari

3-riflessioni sui piani perpendicolari tra loro e

4-rotazioni seguite da riflessioni.
Ritornando adesso al concetto di “elementi equivalenti” di simmetria,  considereremo solamente quelle operazioni che diano una configurazione della molecola equivalente a quella iniziale. Nel caso specifico (H20), le operazioni che daranno configurazioni equivalernti, sono le seguenti:
1) Identità -(E)
2) Rotazione di 2π/3= 120⁰ (oraria) che chiamiamo C3⁺  o semplicemente C3 intorno all’asse passante per il centro del triangolo.
3) Rotazione di 4π/3= 180⁰ (oraria)  C3²⁺ intorno allo stesso asse sopra descritto
4) Rotazione di 2π sull’asse precedente, ma ciò equivale alla identità E. e non deve essere considerata separatamente.
5) Rotazione di 2π/3= 120⁰ (antioraria),cj (essa però èe quivalente a C3⁺così come C3^2— equivalerete a C3 ²⁺
6) Riflessione sul piano perpendicolare a quello su cui giace il triangolo con il vertice  I  (a) al centro σ_v^I  oppure Cv^a
7) riflessione come sopra per b
8) Come sopra per il vertice C.
9) Rotazione seguita da riflessione Sn .
Possiamo allora riassumere le varie operazioni eseguite sul triangolo e le relative configurazioni, in una tabella:

_________________________________________________

|  OPERAZIONE      |        CONFIGURAZIONE

________________________________

E                                          A          B          C

C3⁺                                     C           A          B

C3^–                                      B           C          A

σv^a                                             A           C          B

σv^b                                             C           B          A

σv^c                                               B           A          C

__________________________________

Pertanto, in relazione alle considerazioni fatte, possiamo classificare le molecole triangolari come appartenenti al gruppo di simmetria C3v.

Nel caso cella molecola planare AB2X come ad es. CH2O  si hanno operazioni di rotazioni C2, riflessioni su piani verticali ed il gruppo cui essa appartiene è C2v.

(ricordiamo che l’indice in C3 e C2 rappresenta l’ordine del gruppo)

Nel caso esista un asse Cn perpendicolare ad altri due di ordine 2 (C2) vi saranno 2ⁿ  elementi che formeranno il gruppo che viene indicato come Dn  e se esiste un piano verticale si chiama D_nv se invece il piano è orizzontale il gruppo è D_nh.

Le molecole lineari posseggono un piano di simmetria perpendicolare all’asse che unisce i nuclei, un numero infinito di assi C2 perpendicolari all’asse molecolare ed un centro di inversione i e quindi appartengono ad un gruppo chiamato D∞h   e se il piano non esiste il gruppo è C∞v.

Le molecole a simmetria cubica tetraedrica

possiedono i seguenti elementi di simmetria:

1-tre assi impropri S4 che coincidono con gli assi cartesiani

2- tre assi C2 coincidenti con quelli X,Y,Z

3- quattro assi C3 ognuno passante attraverso un vertice ed il centro della faccia opposta

4- sei piani di simmetria

Questo gruppo è indicato co Td

Le molecole a forma ottaedrica (ad es. PtCl6^-2 )

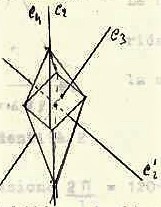
possiedono

1- Tre assi  impropi (S4) passanti ettraverso una coppia di vertici oppost1,

2-Tre assi C2 colineari con S4 e C2 

3-tre assi C4 colineari con S4 e C2

4- sei assi C2′ che bisecano angoli opposti 

5- quattro assi S6 ognuno passante attraverso il centro di una coppia di facce triangolari opposte

6- quattro assi C3 colineari con quelli S6 

7- un centro di inversione i

8- tre piani di simmetria che passa attraverso quattro dei sei vertici

9- sei piani di simmetria passanti attraverso due apici bisecanti due facce opposte

Questo gruppo è chiamato Oh

Possiamo adesso costruire le tavole dei prodotti  (come la tabellina) per esempio per il gruppo C3v si ha :

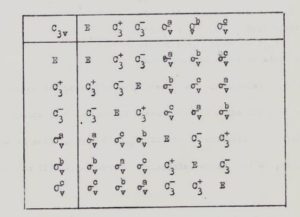
in questo caso

C3+ E =C3+    

C3+C3-= E

C3- C3-=C3+

ecc.

Il numero di elementi di simmetria di tipo diverso appartenente ad un gruppo si chiama CLASSE del gruppo. Per esempio nel gruppo sopra visto C3v vi sono  3 CLASSI  ( E,C3,σ_v).

COME SI ATTRIBUISCE UN GRUPPO AD UNA MOLECOLA?

Prendiamo come esempio H2O

Possiede un asse C2 e non ha assi di ordine più alto.

Non vi sono assi C2 perpendicolari al primo (non può essere perciò D)

Non esistono piani σ_h

esistono due piani verticali σv 

CONCLUSIONE:  la molecola di H2O appartiene al gruppo C_2v

Consideriamo la molecola di ammoniaca NH3

Possiede un asse C3

non vi sono assi S6

non vi sono assi C2 perpendicolari a C3  pertanto il gruppo non può essere D

Non esistono piani σ_h

esistono tre  piani verticali σ_v 

CONCLUSIONE: la molecola appartiene al gruppo C3v

consideriamo adesso l’allene:

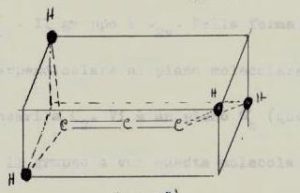
vi è un asse C2 che unisce gli atomi di Carbonio

vi è un asse S4 (improprio cioè rotazione seguita da riflessione) colineare a C2 

Vi sono 2 assi C2 perpendicolari alla linea che unisce i tre atomi di Carbonio (asse C2) quindi per questo la molecola deve appartenere ad un gruppo D 

Non esistono piani σ_h

esistono due  piani verticali σ_v  che passano attraverso gli assi C2

CONCLUSIONE: l’allene appartiene al gruppo D2d 

Consideriamo la molecola H2O2 perossido di idrogeno:

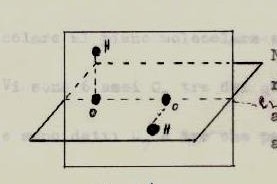
Possiede un asse C2

Non vi sono assi C2 perpendicolari ad un altro asse per cui la molecola è del gruppo C

vi è un asse perpendicolare al piano molecolare 

non vi sono assi S4 colineari a C2

esiste un piano σ_h (quello molecolare)

CONCLUSIONE : H2O2 appartiene al gruppo C_2h

Consideriamo il Benzene C6H6 

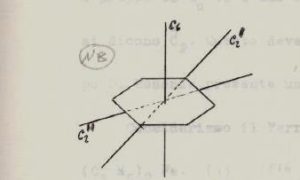
L’asse di ordine più alto è di ordine 6 perpendicolare al piano della molecola e passante attraverso il centro 

Vi sono 6 asi C2 tre dei quali bisecano linee opposte C-C e sono detti assi C’2 e tra che passano attraverso opposti legami CH e si definiscono C”2 

Queto gruppo è quindi di tipo D .

Vi è un piano orizzontale perpendicolare all’asse senario ed il gruppo cui appartiene il Benzene è D_6h

ASPETTI MATEMATICI DELLE OPERAZIONI DI SIMMETRIA

Tutte le operazioni di simmetria descritte sopra possono essere rappresentate matematicamente sotto forma di matrice ed ovviamente dobbiamo conoscere cosa è una matrice e come è possibile eseguire con esse le varie le operazioni.

Una matrice che si indica con il simbolo [   ]  oppure con (  )

è una disposizione rettangolare di numeri , o più in generale di simboli, che obbedisce a determinate regole. Una matrice si può rappresentare nel seguente modo

oppure [a_mn] o anche [a_ij]

il gruppo di elementi verticali è chiamato “colonna” e quello orizzontale “riga” quindi con il termine a_mn 0ppure a_ij indichiamo l’elemento della matrice che occupa la riga m e la colonna j oppure il che è lo stesso la riga i e  la colonna J

Riferendoci alla matrice sopra scritta, gli indici i ed j definiscono il cosiddetto “ordine” della matrice in cui i definisce il numero di righe e j il numero delle colonne . Matrici importanti per la nostra discussione sono le cosiddette matrici quadrate in cui i=j cioè in cui il numero di righe è uguale al numero di colonne.

Sempre riferendoci alla matrice sopra scritta in cui riteniamo i=j , i termini

a₁₁,a₂₂,a_33…..a_ij (ricordiamo che i=j)vengono definiti termini DIAGONALI della matrice  quadrata. Se nella matrice quadrata i termini diagonali sono tutti uguali ad 1 ed i rimanenti termini sono uguali a zero, la matrice è definita “matrice unità”

| 1 0 0 |

|0 1 0 |

|0 0 1 |

OPERAZIONI TRA MATRICI

SOMMA 

la somma di due matrici A  i cui elemento sono aij e B i cui elementi sono bij che sono della stessa dimensione, produce una matrice  C di dimensioni uguali alle precedenti in cui ogni elemento è la somma dei corrispondenti elementi  cioè  Cij = aij + bij

per esempio la somma tra le due matrici quadrate 

SOTTRAZIONE

la sottrazione segue la stessa metodologia della somma infatti 

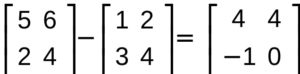
MOLTIPLICAZIONE DI UNO SCALARE (UN NUMERO) PER UNA MATRICE

Il prodotto tra uno scalare X ed una matrice è sempre una matrice in cui ogni elemento aij viene moltiplicato per X

per esempio   

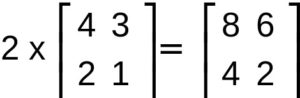
PRODOTTO TRA DUE MATRICI

da cui si evince che in generale il prodotto tra due matrici 

dove

C11 = (a₁₁xb₁₁ ) + (a₁₂xb₂₁)

C12= (a₁₁xb₁₂) +(a₁₂xb₂₂)

C21= (a₂₁x b₁₁ )+(a₂₂xb₂₁)

C22=( a₂₁xb₁₂)+ (a₂₂x b₂₂)

mettiamo in evidenza che A x B =C ma non sempre BxA=C cioè non sempre commutano.

CASO PARTICOLARE DI MOLTIPLICAZIONE TRA BLOCCHI

Consideriamo le due matrici:

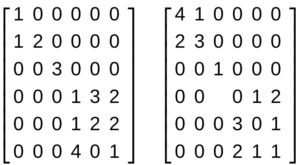
La matrice prodotto sarà formata da una matrice in cui i blocchi lungo le diagonali sono costituiti dai prodotti dei rispettivi blocchi :

 la matrice prodotto avrà quindi i blocchi

$\left[\begin{array}{cccccc}4& 1& & & & \\ 8& 7& & & & \\ & & 3& & & \\ & & & 13& 3& 10\\ & & & 10& 3& 8\\ & & & 20& 5& 9\end{array}\right]$

I CARATTERI DI UNA MATRICE

Si definisce CARATTERE DI UNA MATRICE e si indica con la lettera greca χ la somma degli elementi diagonali della matrice:

χ_[a]= ∑ aij

per la matrice

Cercheremo adesso di individuare quali siano le matrici che rappresentano le rotazioni, le riflessioni e le altre operazioni di simmetria.

ROTAZIONI E MATRICI

Consideriamo un punto in un piano XY: sia X1 l’ascissa ed Y1 l’ordinata. Queste coordinate si riferiscono ad un vettore  r1 compreso tra l’origine ed il punto X1,Y1.

Ruotiamo il vettore r1 di un angolo θ ed otterremo il vettore r2 di coordinate X2,Y2.Queste coordinate sono in relazione con le precedenti coordinate X1,Y1; basta ricordare che la componente x1 del vettore r1  quando ruotato diviene a sua volta un vettore che avrà 2 componenti una su X ed una su Y 

da questa figura si evince che X1 = r1 cos α     e   Y1= r1 sen α 

se ruotiamo il vettore r1 diviene r’1 e l’angolo è Θ =α+θ   quindi

X’1 =r1 cos(α +θ )

X’1= r1  cos α cos θ – r1 sen α senθ   ma

 r1 cos α = X1

r1 senα = Y1    quindi

X’1= X1 cos θ  -Y1 sen θ

Y’1= X1 sen θ + Y1 cos θ

X’1 ed Y’2 possono quindi essere espressi come rotazione di 2 matrici .Più precisamente un vettore può essere rappresentato con una matrice colonna 

$\left[\begin{array}{c}X{‘}_1\\ Y{‘}_1\end{array}\right]$

e se osserviamo il secondo termine dell’uguaglianza scritta sopra vediamo che anche

X1 cos θ  -Y1 sen θ

X1 sen θ + Y1 cos θ possono essere rappresentate con una matrice :

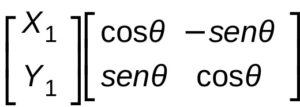
possiamo quindi rappresentare una rotazione di un angolo θ su un pano XY come un prodotto di due matrici

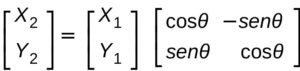
dove X2 Y2 sono rispettivamente X’1 ed Y’1.

 INVERSIONE SU UN PIANO E MATRICI

consideriamo il vettore r1 la riflessione sul piano orizzontale si trasformerà nel vettore r3 con coordinate X3,Y3

e si vede che la coordinata Y cambia di segno e seguendo il ragionamento simile al caso precedente,la matrice inversione è il risultato di una rotazione e di una riflessione.

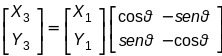
Posssiamo quindi sostenere che ogni operazione di simmetria può essere  rappresentata con matrici di diversa dimensione.

I GRUPPI DI SIMMETRIA E LE TAVOLE DI MOLTIPLICAZIONE

procediamo con un esempio. cONSIDERIAMO UNA MOLECOLA CHE APPARTIENE AL GRUPPO C2v quale ad esempio l’aldeide formica  CH2O. Essa giace su un piano ad es. il piano XY ed avrà le coordinate x,y,0 (zero  perchè non è tridimensionale) se eseguiamo le operazioni di simmetria del gruppo dopo averle effettuate  avremo le coordinate

E =/x,y)

C2 = (-x, -y)

σv = (+x,-y)

σv’= (-x,y)

in forma di matrice si ha

fra tutte le rappresentazioni solo un certo numero di esse posseggono significato speciale e sono le cosiddette “RAPPRESENTAZIONI IRRIDUCIBILI”: risultano infatti per ogni gruppo insiemi completi di matrici più semplici che però non possono essere ridotte ulteriormente .

In conclusione, se abbiamo una rappresentazione di matrici, possiamo decomporla in rappresentazione di matrici più piccole delle precedenti  e questo delle R.I. è un concetto molto utile nell’applicazione della teoria dei gruppi in chimica.Esistono alcune regole sulle R.I. e cioè:

il numero di R.I. di un gruppo  è uguale alle classi del gruppo

la somma dei quadrati delle dimensioni delle R.I. cioè le dimensioni delle matrici è uguale all’ordine del gruppo 

Facciamo un esempio: Sappiamo che il gruppo C3v ha un ordine n=6 ed un numero di classi m=3 (E,C,σ) quindi la somma dei quadrati delle dimensioni delle R.I.del gruppo devono fornire 6 cioè l’ordine del gruppo.

In questo caso specifico i quadrati di 3 numeri (le classi)  devono essere uguali a 6 (l’ordine del gruppo).

1²+1²+2² =6

Per il gruppo C3v la tavola dei caratteri si può scrivere:

la prima rappresentazione Γ₁ è la rappresentazione totalmente simmetrica.

   Send article as PDF