L’ ENTROPIA

IL PRIMO PRINCIPIO  della termodinamica definisce la relazione tra le varie forme di energia presenti in un sistema, il lavoro che il sistema può eseguire e  la quantità  di calore che si sviluppa . Il primo principio  afferma che l’energia è conservata in tutti i processi termodinamici. C’e tuttavia un problema: in natura alcuni fenomeni avvengono spontaneamente ed altri invece necessitano di un intervento esterno.Per esempio, un corpo freddo a contatto con un corpo caldo si riscalda perché il calore fluisce sempre dal corpo più caldo a quello più freddo sino a che la temperatura tra i due corpi non diviene uguale. Alcune reazioni chimiche avvengono in una sola direzione come ad esempio,la combustione del diamante produce CO2 ma la CO2 non riforma spontaneamente il diamante : esistono, quindi, in natura  variazioni spontanee ed altre non spontanee. Ma cosa determina la spontaneità di una variazione in natura? Il primo principio  della termodinamica ΔΕ = Q – PΔV ci dice che in un processo l’energia si può trasformare in calore e lavoro ma si conserva. Tuttavia, osserviamo anche che ogni processo tende sempre a raggiungere uno stato di energia più bassa e quindi apparentemente si ha una perdita di energia. Infatti, se l’ energia di un sistema in esame apparentemente diminuisce occorre tener conto che l’ambiente o universo che circonda il sistema aumenta la propria energia della stessa quantità che viene persa dal sistema. Quando in un sistema avviene una variazione, l’energia totale rimane costante ma varia la sua distribuzione ed è proprio la distribuzione che determina la spontaneità  di un fenomeno. Si deduce quindi che un processo spontaneo è in realtà una conseguenza del fatto che la tendenza naturale dell’Universo è quella di andare verso il Caos o grande disordine. In un processo spontaneo,l’esempio evidente della distribuzione dell’ energia in diverse forme può essere rappresentato da una pallina che rimbalza su un pavimento.Sappiamo tutti che dopo ogni rimbalzo, l’altezza della pallina diminuisce sempre più a causa dell’attrito tra pallina e pavimento e quindi il processo tende a portare la pallina a rimanere, alla fine, ferma sul pavimento avendo trasformato l’energia cinetica in energia potenziale ed avendo perso energia a causa dell’attrito con l’aria e col pavimento. La direzione del fenomeno è sempre diretta verso lo stato di immobilità della pallina e non si è mai osservato che una pallina ferma si metta a rimbalzare da sola sul pavimento.Abbiamo quindi scoperto che la direzione di un fenomeno spontaneo è quella che porta il sistema alla dispersione caotica dell’energia proprio ciò che avviene alla pallina che rimbalza e che disperde l’energia in un numero di modi termici del pavimento ed è impossibile coordinare l’energia dispersa per far avvenire il fenomeno inverso.

Dobbiamo fare una distinzione tra processi irreversibili e processi reversibili(in questi ultimi  gli stati finale ed iniziale differiscono di un infinitesimo per cui è possibile il processo inverso dallo stato finale a quello iniziale. Per esempio consideriamo due gas che si trovano in compartimenti separati ma contigui: sino a che rimangono separati  si ha un certo ordine ma se i compartimenti sono messi in comunicazione  il disordine aumenta in seguito al miscelamento.

Il primo principio della termodinamica usa l’ ENERGIA INTERNA per identificare processi possibili e quindi abbiamo la necessità di definire un SECONDO PRINCIPIO  che ci permetta di stabilire se un processo è spontaneo o meno cioè se un processo è reversibile o irreversibile. Ci chiediamo se esiste un’entità matematica che sia in grado di misurare il grado di disordine di un sistema cioè il grado di dispersione del calore durante un processo. Per individuare questa entità matematica consideriamo un gas che si trova in condizioni isoterme (T=k) ad una pressione P1 e volume V1 che su un grafico Pressione volume indichiamo con A e supponiamo di effettuare una trasformazione reversibile sino a portare i gas dallo stato A ad uno stato B seguendo un percorso che indichiamo con  I

                    P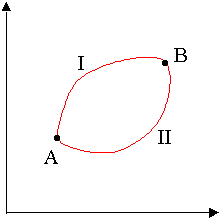  

volume

poi da B sempre in modo reversibile ritorniamo allo stato iniziale  A tramite il percorso II che è diverso da al percorso I.questo significa che  abbiamo effettuato un ciclo reversibile. Lo stato A  è caratterizzato da una pressione p_A e volume V_A, (il volume in figura è  sull’asse delle ascisse= , lo stato Bi è caratterizzato da una pressione P_B  e volume V_B. La linea che congiunge A a B e B ad A non è altro che l’unione di punti che differiscono l’un l’altro di un infinitesimo e per ogni punto cioè in ogni spostamento infinitesimo lungo questa curva si avrà  uno scambio di calore che possiamo indicare  con dQ. Questo scambio di calore avviene ad una certa temperatura T  (dQ sarà positivo se il sistema assorbe calore dall’esterno mentre sarà negativo se cede calore, e se non vi è scambio di calore dQ=0 ). Per arrivare a B partendo da A il calore è dato dalla somma delle quantità dQ per ogni singolo punto sulla curva quindi si può scrivere    dQ/T . Tutte queste quantità  sommate sono rappresentate da un integrale ciclico che si rappresenta con il segno di integrale  con un  cerchietto proprio per indicare che la somma è estesa ad un percorso ciclico. Proprio perché si ha un ciclo, si ha:

$$\begin{gathered} \mathbf{\oint }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{0}\mathbf{ }\mathit{p}\mathit{e}\mathit{r}\mathbf{ }\mathit{u}\mathit{n}\mathbf{ }\mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{s}\mathit{s}\mathit{o}\mathbf{ }\mathit{r}\mathit{e}\mathit{v}\mathit{e}\mathit{r}\mathit{s}\mathit{i}\mathit{b}\mathit{i}\mathit{l}\mathit{e} \\ \mathbf{\oint }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{<}\mathbf{0}\mathbf{ }\mathit{p}\mathit{e}\mathit{r}\mathbf{ }\mathit{u}\mathit{n}\mathbf{ }\mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{s}\mathit{s}\mathit{o}\mathbf{ }\mathit{i}\mathit{r}\mathit{r}\mathit{e}\mathit{v}\mathit{e}\mathit{r}\mathit{s}\mathit{i}\mathit{b}\mathit{i}\mathit{l}\mathit{e}\mathbf{ } \end{gathered}$$

Questo è l’integrale di Clausius. L’integrale di Clausius assume valore pari a zero in un percorso reversibile come nel caso in esame ed è minore di zero in un processo irreversibile.

. Consideriamo allora proprio il ciclo  A-B-A con tutte trasformazioni reversibili. L’integrale di Clausius si può scrivere

$$\begin{gathered} \mathbf{\oint }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{A}}^{\mathbf{B}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{\int }}_{\mathbf{B}}^{\mathbf{A}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{0}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{c}\mathit{i}\mathit{o}\mathit{è} \\ {\mathbf{\int }}_{\mathbf{A}}^{\mathbf{B}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{–}{\mathbf{\int }}_{\mathbf{B}}^{\mathbf{A}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{ }\mathbf{ }\mathit{c}\mathit{i}\mathit{o}\mathit{è} \\ {\mathbf{\int }}_{\mathbf{A}}^{\mathbf{B}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{A}}^{\mathbf{B}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ } \end{gathered}$$

questo significa che la quantità Q/T è una quantità che non dipende dal percorso effettuato ma esclusivamente dallo stato iniziale e finale. Ciò comporta che la quantità Q/T è UNA FUNZIONE DI STATO CHE  VIENE CHIAMATA ENTROPIA ED INDICATA CON S.

Questo vuol dire che nel caso del ciclo possiamo scrivere

${\mathbf{\int }}_{\mathbf{A}}^{\mathbf{ }\mathbf{B}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathit{S}\mathit{B}\mathbf{–}\mathbf{ }\mathit{S}\mathit{A}$

il che ci permette di scrivere anche:

$\mathit{d}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{d}\mathit{q}\mathbf{/}\mathit{T}$

Ricordando  che per il primo principio ,in un processo  reversibile si ha  dE = dq -Pdv dove P=n RT/V e per  un processo isotermo dE=0  possiamo scrivere che:

dq=nRT/V   e

dq/T = nRdV/V  

dS= nRdV/V

Pertanto  la variazione di entropia in un processo reversibile è:

dS= nRln V2/V1

NEL PROCESSO REVERSIBILE DESCRITTO SOPRA CON PERCORSO DALLO STATO  A  ALLO STATO  B SI HA:

ΔS = nR ∫dV/V      da cui    S_B – S_A = nR ln V_B/V_A  =  nR ln VB- lnVA

Esempio

Un campione di idrogeno è contenuto in un cilindro con pistone a stretta tenuta di 50 cm² ; il volume iniziale a 25°C è 500 ml (0,5 litri) alla pressione di 2 atm. Calcolare la variazione di entropia quando il pistone è isotermicamente spostato di 10 cm.

soluzione

il numero di moli di idrogeno è n= PV/RT = 2 x 0,50 / 0,0821 x 298,15  = 0,041 moli

ΔS =( 0,041 mol x 8,314 j/K ln (1000 ml /500 ml ) = 0,34 J/K mol x ln 2 = 0,24 J/K mol 

Consideriamo adesso un sistema ciclico simile a quello descritto sopra ma con un percorso A→ B irreversibile ed uno BA reversibile.

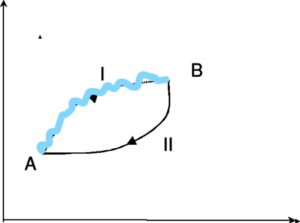
Sappiamo che

$$\begin{gathered} \mathbf{\oint }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{0}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{s}\mathit{e}\mathbf{ }\mathit{i}\mathit{l}\mathbf{ }\mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{s}\mathit{s}\mathit{o}\mathbf{ }\mathit{è}\mathbf{ }\mathit{r}\mathit{e}\mathit{v}\mathit{e}\mathit{r}\mathit{s}\mathit{i}\mathit{b}\mathit{i}\mathit{l}\mathit{e} \\ \mathbf{\oint }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{<}\mathbf{ }\mathbf{0}\mathbf{ }\mathit{s}\mathit{e}\mathbf{ }\mathit{i}\mathit{l}\mathbf{ }\mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{s}\mathit{s}\mathit{o}\mathbf{ }\mathit{è}\mathbf{ }\mathit{i}\mathit{r}\mathit{r}\mathit{e}\mathit{v}\mathit{e}\mathit{r}\mathit{s}\mathit{i}\mathit{b}\mathit{i}\mathit{l}\mathit{e}\mathbf{ } \end{gathered}$$

consideriamo il processo irreversibile

$$\begin{gathered} \mathbf{\oint }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{<}\mathbf{ }\mathit{o}\mathbf{ } quindi se consideriamo il ciclo completo A–B–A \\ \mathbf{\oint }\mathbf{ }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{A}}^{\mathbf{B}}\mathbf{ }\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathit{i}\mathit{r}\mathit{r}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{ }{\mathbf{\int }}_{\mathbf{B}}^{\mathbf{A}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathit{r}\mathit{e}\mathit{v}\mathbf{ }\mathbf{ }\mathbf{<}\mathbf{ }\mathbf{0} \end{gathered}$$

portando l’integrale

$\mathbf{ }\mathbf{ }{\mathbf{\int }}_{\mathbf{B}}^{\mathbf{A}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{ }\mathit{a}\mathit{l}\mathbf{ }\mathit{s}\mathit{e}\mathit{c}\mathit{o}\mathit{n}\mathit{d}\mathit{o}\mathbf{ }\mathit{m}\mathit{e}\mathit{m}\mathit{b}\mathit{r}\mathit{o}\mathbf{ }\mathit{c}\mathit{a}\mathit{m}\mathit{b}\mathit{i}\mathit{a}\mathbf{ }\mathit{d}\mathit{i}\mathbf{ }\mathit{s}\mathit{e}\mathit{g}\mathit{n}\mathit{o}\mathbf{ }\mathit{e}\mathbf{ }\mathit{q}\mathit{u}\mathit{i}\mathit{n}\mathit{d}\mathit{i}\mathbf{ }\mathit{p}\mathit{o}\mathit{s}\mathit{s}\mathit{i}\mathit{a}\mathit{m}\mathit{o}\mathbf{ }\mathit{s}\mathit{c}\mathit{r}\mathit{i}\mathit{v}\mathit{e}\mathit{r}\mathit{e}$ ${\int }_A^{B}dQ/T rev = S_B – S_{A }> {\int }_A^{B}dQ/T irrev$

   ΔS = S_A – S_B > 

${\mathbf{\int }}_{\mathbf{A}}^{\mathbf{B}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathit{i}\mathit{r}\mathit{r}$

 

Consideriamo adesso il sistema in esame (un cerchio) circondato dal suo ambiente : il tutto costituisce un Universo che in questo caso è isolato cioè non scambia nè energia nè materia con l’ambiente esterno all’Universo considerato:

 

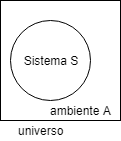
l’universo di cui parliamo non è da intendere come l’Universo cosmologicamente ma semplicemente come l’insieme del sistema e dell’ambiente che lo circonda.Ciò ci serve a comprendere il significato della diseguaglianza

ΔS = S_A – S_B > 

${\mathbf{\int }}_{\mathbf{A}}^{\mathbf{B}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{ }\mathit{i}\mathit{r}\mathit{r}\mathit{e}\mathit{v}$

 

andiamo a calcolare la variazione del’entropia dell’Universo in considerazione che sarà  ΔS> 

${\int }_{univ}dQ/T$

irrev

tuttavia l’universo è isolato quindi dQ =0 pertanto

 

${\mathbf{\int }}_{\mathbf{u}\mathbf{n}\mathbf{i}\mathbf{v}}\mathit{d}\mathit{Q}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{0}$

 

     ΔS_univ  = ΔS _sistema  +  ΔS _ambiente   > 0

Quindi in un sistema generico è sempre valida la disuguaglianza scritta sopra. Tuttavia nel caso in cui come sistema si ha una macchina termica  che funziona su un percorso ciclico, in questo caso essendo l’entropia una funzione di stato la variazione di entropia del sistema

 ΔS _sistema  = 0

il che significa che nel caso in cui si verifica un processo irreversibile l’entropia dell’ambiente è

ΔS _ambiente   > 0

quindi l’entropia dell’universo aumenta.

 

VARIAZIONE DI ENTROPIA CON LA  TEMPERATURA, PRESSIONE ,IL VOLUME E LO STATO FISICO

In un processo reversibile, in relazione al primo principio della termodinamica si ha : dQ=dE + PdV  e sappiamo anche che dQ=TdS per cui   TdS = dE+ PdV ma  H= E+PV per cui differenziando si ha 

dH dE+ PdV + VdP  pertanto possiamo scrivere    TdS = dH -VdP

VARIAZIONE DI ENTROPIA CON LA  TEMPERATURA

in un processo reversibile a volume costante  essendo dQ=dE + PdV  ed essendo dV=0 si ha dQ=dE =TdS 

Sappiamo inoltre che dE= Cv dt quindi   TdS = CvdT  quindi 

dS= CvdT/T 

per una variazione finita a volume costante la variazione di entropia è:

${\mathbf{\int }}_{\mathbf{1}}^{\mathbf{2}}\mathit{d}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{S}\mathbf{2}\mathbf{–}\mathit{S}\mathbf{1}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}}\mathit{C}\mathit{v}\mathbf{ }\mathit{d}\mathit{t}\mathbf{/}\mathit{T}$

cioè

$\mathbf{∆}\mathit{S}\mathbf{=}\mathbf{ }\mathit{C}\mathit{v}\mathbf{ }\mathit{l}\mathit{n}\mathbf{ }{\mathit{T}}_{\mathbf{2}}\mathbf{/}{\mathit{T}}_{\mathbf{1}}$

in un processo reversibile a pressione costante 

dH= TdS

essendo dP=0  per cui

dH= Cp dT 

TdS= CpdT

dS= Cp dT/T

da cui per una variazione finita si ha

$$\begin{gathered} {\mathbf{\int }}_{\mathbf{1}}^{\mathbf{2}}\mathit{d}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{S}}_{\mathbf{2}}\mathbf{ }\mathbf{–}\mathbf{ }{\mathit{S}}_{\mathbf{1}}\mathbf{ }\mathbf{=}\mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}}\mathit{C}\mathit{p}\mathbf{ }\mathit{d}\mathit{T}\mathbf{/}\mathit{T} \\ \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}\mathbf{ }}\mathit{d}\mathit{T}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{C}\mathit{p}\mathbf{ }\mathbf{ln}\mathit{T}\mathbf{2}\mathbf{/}\mathit{T}\mathbf{1} \\ \mathit{e}\mathbf{ }\mathit{p}\mathit{e}\mathit{r}\mathbf{ }\mathit{n}\mathbf{ }\mathit{m}\mathit{o}\mathit{l}\mathit{i}\mathbf{ }\mathit{d}\mathit{i}\mathbf{ }\mathit{s}\mathit{o}\mathit{s}\mathbf{tan}\mathit{z}\mathit{a}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{∆}\mathit{S}\mathbf{=}\mathbf{ }{\mathit{S}}_{\mathbf{T}\mathbf{2}}\mathbf{–}{\mathit{S}}_{\mathbf{T}\mathbf{1}}\mathbf{=}\mathit{n}\mathbf{ }\mathit{C}\mathit{p}\mathbf{ }\mathbf{ln}\mathit{T}\mathbf{2}\mathbf{/}\mathit{T}\mathbf{1} \end{gathered}$$

in assenza di transizioni di fase.

Se Cp dipende dalla temperatura secondo la relazione CP= a + bT +cT²

allora si ha

$$\begin{gathered} \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}\mathbf{ }}\mathbf{(}\mathit{a}\mathbf{+}\mathbf{ }\mathit{b}\mathit{T}\mathbf{+}\mathbf{ }\mathit{c}{\mathit{T}}^{\mathbf{2}}\mathbf{)}\mathit{d}\mathit{T}\mathbf{/}\mathit{T}\mathbf{ } \\ \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}\mathbf{ }}\mathbf{(}\mathit{a}\mathbf{/}\mathit{T}\mathbf{+}\mathbf{ }\mathit{b}\mathbf{+}\mathbf{ }\mathit{c}{\mathit{T}}^{}\mathbf{)}\mathit{d}\mathit{T} \\ \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{a}\mathit{l}\mathit{n}{\mathit{T}}_{\mathbf{2}}\mathbf{/}{\mathit{T}}_{\mathbf{1}}\mathbf{ }\mathbf{+}\mathit{b}\mathbf{(}\mathbf{ }{\mathit{T}}_{\mathbf{2}}\mathbf{–}{\mathit{T}}_{\mathbf{1}}\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{C}\mathbf{/}\mathbf{2}\mathbf{ }\mathbf{(}{{\mathit{T}}^{\mathbf{2}}}_{\mathbf{2}}\mathbf{ }\mathbf{–}\mathbf{ }{{\mathit{T}}^{\mathbf{2}}}_{\mathbf{1}}) \end{gathered}$$

In una REAZIONE CHIMICA 

ΔS _reaz=∑ S_prodotti – ∑S_reagenti 

l’effetto della temperatura sull’entropia di una reazione chimica è:

ricordando che  dH= CpdT

d(ΔH)= ΔCpdT

ma dQ= Td(ΔS)  = d(ΔH)

Td(ΔS) = ΔCpdT

dove ΔH = variazione di entalpia della reazione e ΔCp la variazione termica a P=K associata alla reazione.

Per una variazione finita si ha :

$$\begin{gathered} {\mathbf{\int }}_{\mathbf{1}}^{\mathbf{2}}\mathit{d}\mathbf{(}\mathbf{∆}\mathit{S}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{∆}{\mathit{S}}_{\mathbf{T}\mathbf{2}}\mathbf{–}\mathbf{ }\mathbf{∆}{\mathit{S}}_{\mathbf{T}\mathbf{1}}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}}\mathbf{ }\mathbf{∆}\mathit{C}\mathit{p}\mathbf{ }\mathit{d}\mathit{T}\mathbf{/}\mathit{T} \\ \mathit{s}\mathit{e}\mathbf{ }\mathit{t}\mathit{r}\mathit{a}\mathbf{ }\mathit{T}\mathbf{1}\mathbf{ }\mathit{e}\mathbf{ }\mathit{T}\mathbf{2}\mathbf{ }\mathit{C}\mathit{p}\mathbf{ }\mathit{è}\mathbf{ }\mathit{c}\mathit{o}\mathit{s}\mathit{t}\mathit{a}\mathit{n}\mathit{t}\mathit{e}\mathbf{ }\mathit{s}\mathit{i}\mathbf{ }\mathit{p}\mathit{u}\mathit{ò}\mathbf{ }\mathit{s}\mathit{c}\mathit{r}\mathit{i}\mathit{v}\mathit{e}\mathit{r}\mathit{e} \\ \mathbf{∆}{\mathit{S}}_{\mathbf{T}\mathbf{2}}\mathbf{–}\mathbf{ }\mathbf{∆}{\mathit{S}}_{\mathbf{T}\mathbf{1}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{∆}\mathit{C}\mathit{p}\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}\mathbf{ }}\mathit{d}\mathit{T}\mathbf{/}\mathit{T} \\ \mathbf{∆}{\mathit{S}}_{\mathbf{T}\mathbf{2}}\mathbf{–}\mathbf{ }\mathbf{∆}{\mathit{S}}_{\mathbf{T}\mathbf{1}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{∆}\mathit{C}\mathit{p}\mathbf{ }\mathit{l}\mathit{n}\mathit{T}\mathbf{2}\mathbf{/}\mathit{T}\mathbf{1} \end{gathered}$$

 

VARIAZIONE DI ENTROPIA CON LA PRESSIONE

Dalla relazione

TdS = dH – VdP 

essendo

dH =CpdT 

TdS= CpdT- VdP 

dS = Cp dT/T -V/TdP

ma per un gas perfetto si ha    PV= nRT  perciò    per 1 mole  V/T = R/P  quindi

 

dS = Cp dT/T –  R dP/P

in una trasformazione isoterma si ha  dS= -RdP/P ed integrando tra P1 e P2

ΔS= S2 -S1= -R lnP2/P1  e per n moli

ΔS= S2 -S1= – nR lnP2/P1

e se integriamo ds=-RdP/P tra lo stato standard e la pressione P si ha

S – S° = -RlnP      S= S° -RlnP

 

VARIAZIONE DI ENTROPIA IN FUNZIONE DELLA TEMPERATURA E DELLA PRESSIONE 

dS= Cp dT/T – R dP/P

integrando si ha

$$\begin{gathered} \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\int }}_{\mathbf{T}\mathbf{1}}^{\mathbf{T}\mathbf{2}\mathbf{ }}\mathit{C}\mathit{p}\mathit{d}\mathit{T}\mathbf{/}\mathit{T}\mathbf{ }\mathbf{–}\mathbf{ }\mathit{R}\mathbf{ }\mathit{l}\mathit{n}\mathit{P}\mathbf{2}\mathbf{/}\mathit{P}\mathbf{1}\mathbf{ } \\ \mathbf{∆}\mathit{S}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{C}\mathit{p}\mathbf{ }\mathit{l}\mathit{n}\mathbf{ }\mathit{T}\mathbf{2}\mathbf{/}\mathit{T}\mathbf{1}\mathbf{ }\mathbf{–}\mathbf{ }\mathit{R}\mathit{l}\mathit{n}\mathit{P}\mathbf{2}\mathbf{/}\mathit{P}\mathbf{1}\mathbf{ }\mathbf{ }\mathbf{ }\mathit{s}\mathit{e}\mathbf{ }\mathit{C}\mathit{p}\mathbf{ }\mathit{è}\mathbf{ }\mathit{c}\mathit{o}\mathit{s}\mathit{t}\mathit{a}\mathit{n}\mathit{t}\mathit{e}\mathbf{ }\mathit{t}\mathit{r}\mathit{a}\mathbf{ }\mathit{T}\mathbf{1}\mathbf{ }\mathit{e}\mathbf{ }\mathit{T}\mathbf{2} \end{gathered}$$

VARIAZIONE DI ENTROPIA CON IL VOLUME

TdS = dE + PdV

ma dE= CvdT 

TdS= CvdT + PdV 

dS= CvdT/T + P/T dV

ma PV=nRT

P/T =R/V  e sostituendo

dS= CvdT/T +RdV/V 

e per un processo isotermo 

dS=R dV/V  

ΔS = S2-S1 = RlnV2/V1

la variazione di entropia con la temperatura e col volume, è

dS= Cv dT/T +R dV/V 

integrando se Cv = k si ha

 ΔS = Cv lnT2/T1 + RlnV2/V1

 

VARIAZIONE DI ENTROPIA IN FUNZIONE DELLO STATO FISICO

supponiamo che vi sia una trasformazione reversibile  e che decorra a P=K ed alla temperatura di equilibrio allora

    dS=dQ _rev / T

 dS=dH / T

ΔS= ΔH / T