ESERCIZI SULLA f.e.m. DELLE PILE

1-Calcolare la fem della pila    Zn/zn+2 0,01 ||Pb+2 0,06 M/Pb

E°zn= -0,76 V

E°Pb = -0,13 V

pertanto Ezn = -0,76 + 0,06/2 log 10^-2  = -0,76 -2 x 0,06/2 = 0,76 –  x -2 x 0,03

Ezn=- 0,76-0,06 = – 0,82 V

EPb= -0,13 + 0,06/2 log 6 x 10^-2 = – 0,13 – 0,06 log 6 = -0,13  -0,047 =- 0,177 V

f.e.m. = Ecat – Ean= Epb

il catodo è l’elettrodo diPb in quanto E=- 13  è più positivo dell’elettrodo di Zn E°= -0,176

quindi f.e.m. =  EPb- EZn

fem= -0,177 -(-0,82)= 0,64 V 

2  Indicare gli schemi dei semielementi formati dalle seguenti semireazioni  e scrivere la corrispondente equazione di Nernst:
a) 2H3O+ + 2e- → H2 (g) + 2 H2O

b) Al3+ + 3e- → Al(s)

c) O2(g) + 4 H3O+ + 4e- → 6 H2O

d) MnO4- + 5e- + 8 H3O+ → Mn2+ + 12 H2O

soluzione

a) per l’elettrodo ad idrogeno sappiamo che E°=0 per convenzione 

           Pt (H2 (g))/ H3O+                   E_H3O+/H2= 0 + 0,06/2 log [H3O+]² / P_H2

b)       Al/Al+3                                        E_Al3+/Al = E°_Al3+/Al + 0,06/3 log [Al+3]

c)       Pt _{[O2 (g)]/H3O+}                                E_{O2/ H2O} = E°_{O2/ H2O +} 0,06/4 log Po2 [h3O+]²

d)       Pt /MnO4-, Mn2+, H3O+       

                                 E _MnO4-/Mn+2 = E° _MnO4-/Mn+2 + 0,06/5 log [MnO4-][H+]⁸ / [MN+2]

3- Calcolare il potenziale dei seguenti semielementi:

a) Pt /SnCl2 0,10 M, SnCl4 0,010 M                      E°_Sn4+/Sn2+ = 0,13 V

Sn4+ + 2e- → Sn2+           E_Sn4+/Sn2+ = E°_Sn4+/Sn2+ +0,06/2 log[Sn+4]/[Sn+2]

                                                     E_Sn4+/Sn2+ = 0,13 +0,06/2 log 0,01/0,1  =0,10 V 

b)  Ni /NiCl2 0,010 M                     E°_Ni2+/Ni = -0,25 V

Ni2+ + 2e- → Ni                             

E_Ni2+/Ni = E°_Ni2+/Ni +0,06/2 log[Ni2+] = -0,25+0,06/2 log 0,01 = 0,31 V

c)   Ni /NiS (sol. satura)                  E°_Ni2+/Ni = -0,25 V              Kps _NiS = 1,0 x10^-22

NiS(s)→ Ni²⁺(aq)+S^2-(aq)           Kps= [Ni²⁺][S^2-]=s² [Ni2+] = s =√Kps=√1,0 x10^-22

Ni2+ + 2e- →Ni

E_Ni2+/Ni = E°_Ni2+/Ni   + 0,06/2 log[Ni⁺²]=-0,25+ 0,06/2log 10^-11 = 0,575 V

5- Calcoliamo la costante di equilibrio relativa alla dismutazione Cu⁺_(aq) → Cu_(s) + Cu²⁺_(aq) a 298 K, sapendo che

E°(Cu⁺/Cu) = +0,520 V

E°(Cu²⁺/Cu) = +0,340 V

La dismutazione è la somma delle seguenti due semireazioni

Riduzione        Cu⁺_(aq) + e^– →  Cu_(s)

Ossidazione     Cu⁺_(aq) →  Cu²⁺_(aq)    + e^–

per calcolare la Keq è necessario conoscere il potenziale di riduzione della coppia redox Cu^2+/Cu⁺ combinando opportunamente i due potenziali noti. Se consideriamo la reazione

Cu⁺_(aq) →  Cu²⁺_(aq)    + e^–   possiamo notare che è possibile ottenerla sommando le due reazioni viste sopra

1[Cu²⁺ +   2e → Cu                     E° = + 0,340 V

2[Cu → Cu⁺  + e      =                  E° = – 0,520 V( la reazione  è una ossidazione)

Cu²⁺ + e → Cu⁺

Moltiplichiamo ciascun potenziale per il numero di elettroni della relativa semireazione e sommando

(+ 0,340 x 2) + (- 0,520 x 1) = + 0,160 V

Il potenziale così ottenuto va diviso per il numero di elettroni della semireazione finale

E°(Cu²⁺/Cu⁺) = + 0,160 : 1 = 0,160 V

Ora possiamo calcolare il potenziale in condizioni standard della reazione complessiva di dismutazione come differenza tra il potenziale di riduzione della reazione catodica (semireazione di riduzione)  e di quella anodica (semirazione di ossidazione)

E°Pila = E°cat – E°an = 0,520 – 0,160 = + 0,360 V 

La costante di equilibrio è data da :

0 =   E° pila x 0,0591/n log Keq                     logKeq=n(E°pila) / 0,0591   n=1

log keq= 0,360/0,0591  = 6,1

Keq=1,26 x 10⁶

6-Calcoliamo la costante di equilibrio relativa alla dismutazione

3 ClO^–_(aq) →  2 Cl^–_(aq) + ClO₃^–_(aq)  

in ambiente basico a 298 K, sapendo che il potenziale standard delle seguenti semireazioni di riduzione

ClO₃^–_(aq)  + 3H₂O + 6e- → Cl^– + 6OH^–            E°( ClO₃^–/ Cl^–)  =   + 0,62 V

ClO^–_(aq)  + H₂O + 2e- → Cl^– + 2OH^–               E°( ClO^–/ Cl^–)   =   + 0,89 V

La dismutazione è la somma delle seguenti due semireazioni

Riduzione        2ClO^–_(aq) + 4e- → 2Cl^–       E° =  + 0,89 V

Ossidazione     ClO^–_(aq) → ClO₃^– + 4e          E° = sconosciuto

Dobbiamo calcolare il potenziale di riduzione della coppia redox ClO₃^–/ ClO^– , che caratterizza la semireazione di ossidazione, combinando opportunamente i due potenziali noti. La semireazione di riduzione desiderata si può ottenere come somma delle seguenti due semirazioni

ClO₃^–_(aq)  + 3H₂O + 6e- → Cl^– + 6OH^–           E° = + 0,62 V

Cl^– + 6OH^–  → ClO^–_(aq)  + H₂O + 2e                E° = – 0,89 V (il segno è cambiato perché è un’ ossidazione)

────────────────────────

ClO₃^–_(aq)  + 2H₂O + 4e- → ClO^– + 4OH^–          E° = [(0,62 x 6)+(-0,89 x 2)] / 4 = 0,485 V

Il potenziale della coppia redox ClO₃^–/ ClO^–  si ottiene sommando i potenziali delle due semireazioni ciascun potenziale moltiplicato per il numero di elettroni della relativa semireazione. Il potenziale così ottenuto va diviso per il numero di elettroni della semireazione-somma (4 elettroni)

Ora possiamo calcolare il potenziale in condizioni standard della reazione complessiva di dismutazione come differenza tra il potenziale di riduzione della reazione catodica (semireazione di riduzione)  e di quella anodica (semirazione di ossidazione)

E°cat – E°an = 0,89 – 0,485 = + 0,405 V

Essendo il numero di elettroni scambiati nella reazione bilanciata di dismutazione pari a  n = 4, la costante di equilibrio varrà

 log Keq = 4 x 0,405 /0,0591 = 27,41   

Keq= 1,29 x 10²⁷

7- Quando l’ossigeno esercita la sua azione ossidante, esso può ridursi ad acqua ossigenata (O2→H2O2), e questa poi ad acqua (H2O2 →HzO), oppure ridursi direttamente ad acqua (O2→H2O). Noti i valori dei potenziali standard E°O2/H2O2, = 0,682 V ed E°H2O2/H2O = 1,776 V, si calcoli il valore del potenziale standard della riduzione diretta E° O2 /H,O .

Le semireazioni sono:

O2+2H3O⁺+2e →H2O2+2H2O   (E^o=O,682 V)

H2O2+2H3O⁺ +2e → 4H2O          (E^o= 1,776 V)

sommando ambedue le reazioni:

O2+4H3O⁺  +4 e → 6H2O    E°x= ?

che è la riduzione diretta  e l’energia di quest’ultima è quindi la somma delle energie delle semireazioni

ΔG°_{ultima reazione} = ΔG°_{prima semireazione} + ΔG° _{seconda semireazione}

sappiamo però che        -ΔG° = nFE°

quindi

[ – 2 x F x 0,682] – [2 x F x 1,774] = = – 4x Fx E°x

da cui

E°x = 1,23 V

7- Alla temperatura di 25,0 °C, la I.e.m. della pila

     Pt(Cl₂) / Cl- ||  Cu+2 /Cu

(pCl2 = 1 atm)  [Cl-] = 0,001M  [Cu+2] = 0,1M        

ΔE = 1,256 V. Calcolare  la costante dell’ equilibrio  Cl₂+ Cu <=>2Cl- + Cu²

sappiamo che        logKeq= n(Eox-Erid) / 0,0591

essendo Eox-Erid= f.e.m Epila ed essendo Epila= 1,256 V si ha

1,256= [E° Cl2/2Cl-  -0,0591 x log 10^-3  ] –  [E°Cu+2/Cu  + 0,0591\/2 log 10^-1 ]  da cui

E° Cl2/2Cl-  –   E°Cu+2/Cu =1,049V

log Keq = 2 x 1,049 / 0,0591 = 35,50

Keq= 3,2 x 10^-35

6- Stimare la stabilità dell’acqua in condizioni standard a pH = 7 e a pH = 3, considerando le due semireazioni.

(Stabilità dell’acqua significa la tendenza che ha l’H2O a scindersi nei suoi due componenti cioè O2 ed H2). Sappiamo che:

O₂ + 2H₂O + 4e →4OH^–                    E°(O₂/OH^–) = + 0,401 V

2H⁺ + 2e  → H₂                                     E°(H⁺/H₂) = 0 V

soluzione

Il potenziale della prima semireazione è dato in condizioni standard e quindi per [OH^–] = 1 M e dunque un pH = 14. La dipendenza di tale potenziale dal pH per 1 atm di pressione è

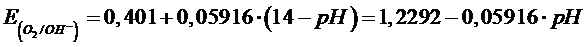
Il potenziale della seconda semireazione è dato in condizioni standard e quindi per [H⁺] = 1 M e dunque un pH = 0. La dipendenza di tale potenziale dal pH per 1 atm di pressione è

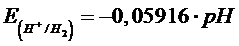
Al variare del pH i due potenziali variano quindi nello stesso modo (al crescere del pH decrescono) e della stessa quantità (una variazione di 0,05916 V per ogni punto di pH)

La prima semireazione manterrà dunque a qualsiasi pH un potenziale superiore alla seconda e quindi la prima si ridurrà a spese della seconda che si ossiderà.

La reazione spontanea complessiva sarà

Riduzione       O₂ + 2H₂O + 4e → 4OH^{–                                 +}

Ossidazione    2H₂  →  4H⁺ + 4e                    

             ──────────────────────────

Totale              O₂ + 2H₂  →  2H₂O

Infatti 4H+ +4OH- del secondo membro è ugale a  2H2O che si semplifica con 2H2O del primo membro

Il potenziale complessivo (potenziale di cella) è  indipendente dunque dal pH

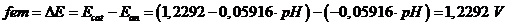
La costante di equilibrio della reazione totale sarà

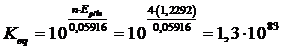
Il potenziale della reazione opposta, avrà lo stesso valore ma segno opposto

2H₂O →  O₂ + 2H₂    E = – 1,2292 V

La costante di tale equilibrio, che ci informa della tendenza dell’acqua a scindersi negli elementi che la costituiscono (e quindi della sua stabilità), è

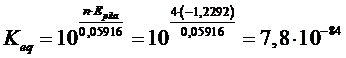
che è così piccolo da poter dire che l’acqua non ha praticamente alcuna tendenza a scindersi negli elementi che la costituiscono.

8- Indicare gli schemi dei semielementi formati dalle seguenti semicoppie redox e scrivere la corrispondente equazione di Nernst:

a) 2 H3O+ + 2e- → H2 (g) +2 H2O

schema : Pt (H2 (g))/ H3O+ H3O+/H2 

Nernst:  E_H3O+/_H2=    0,059/2 log [H3O+]² /P_H2

b) Al3+ + 3e- →Al(s)                   

schema :Al/Al3+                         

Nernst :  E_Al3+/Al = E°_Al3+/Al   +  0,059 /3 log [Al+3]

c) O2(g) + 4 H3O+ + 4e- → 6 H2O

schema :Pt (O2 (g))/H3O+  

 Nernst: E_{O2/ H2O} = E°_{O2/ H2O}  + 0,059/4 logPO2 [ H3O+]²

d) MnO4- + 5e- + 8 H3O+ →Mn2+ + 12 H2O       

schema: Pt /MnO4-, Mn2+, H3O+

Nernst :

E_MnO4-/Mn+2 =E°_MnO4-/Mn+2   + 0,059/5 log[MnO4-] [H3O+]⁸  / [Mn+2]

7- Calcolare la f.e.m. delle seguenti pile:

a) Fe/Fe2+ 0,10 M ||Fe2+ 0,50 M; Fe3+ 0,050 M /Pt

sapendo che :
E°Fe2+/Fe= -0,44 V

E°Fe3+/Fe2+ = 0,80 V

al polo positivo si ha
Polo + Fe3+ + e- →Fe2+
E_{polo +} = E_Fe3+/Fe2+ = E°_Fe3+/Fe2+ +0,059 log[Fe+3]/[Fe+2]

E_{polo +} = = 0,80+0,059log  0,05/0,5 = 0,74 V

Al polo negativo si ha :

Polo neg. –     Fe2+ + 2 e- → Fe
E_polo –= E_Fe2+/Fe= E°_{Fe2+/Fe + 2} +0,059  log[Fe2+] = -0,44 + 0,059/2  log0,1= -0,47 V

E_pila = E_p0lo+ – E_polo-        

Epila = 0,74-(-0,47)= 1,21 V

b) Pt (H2 p = 1,0 atm) / H2SO4 0,050 M || AgNO3 0,10 M/Ag

E°Ag+/Ag = 0,80 V

al polo positivo
Polo + Ag+ + e-  →Ag

E+= E_Ag+/Ag = E°_Ag+/Ag + 0,059 log[Ag+]= 0,8 + 0,059 log 0,1= 0,74 V

al polo negativo

Polo –     2 H3O+ + 2e- →  H2 (g) + 2 H2O

PH2=1,0 atm [H3O+]=2H2SO4= 2×0,05 = 0,1 M

E° _H3O+/H2-= 0

E_{polo neg} = E_H3O+/H2= 0,059/2 log[H3O+]² / PH₂

E_{polo neg}= 0,059log[H3O+]= 0,059 log0,1= –0,059 V

E_pila = Epolo p0sitivo – Epolo negativo = 0,74-(-0,059)= 0,80 V

c) Pt (H2 p = 2,0 atm) /CH3COOH 0,10 M || AgCl(sol. satura) /Ag

E°Ag+/Ag = 0,80 V                                 ⇄

Ka= 1,8 x10-5                     Kps AgCl = 1,5 x10-10

il polo positivo è 
Polo +             Ag+ + e- → Ag
AgCl(s)  ⇄ Ag+(aq) + Cl-(aq) da cui si evince

[Ag+] = [Cl-] = √ Kps          poichè Kps = [Ag+][Cl-]=S²
[Ag+] = s = √ Kps =√1,7 x  10^-10=1,3×10-5 M

pertanto
Epolo+= E_Ag+/Ag = E°_Ag+/Ag + 0,059l og[Ag+]= 0,8 + 0,059 log 1,3×10^-5= 0,51 V

il polo negativo è:
Polo – 2 H3O+ + 2e- → H2 (g) + 2 H2O

P_H2=2,0 atm         E° _H3O+/H2= 0

CH3COOH + H2O ⇄CH3COO- + H3O+      [H3O+] =√Kax Ca =√1,8 x 10^-5 x 0,1 = 1,3 x 10^-3

Epolo neg -= E_H3O+/H2=0,059/2 log (1,3 x 10^-3)²/2 =  0,059 log 0,1= -0,15 V

Epila = E+- E-= 0,51-(-0,15)= 0,66 V 

8- Calcolare quale deve essere la concentrazione dello ione Ag+ perché la f.e.m. della pila sia pari a
zero, sapendo che E°_Fe+3/Fe+2 = 0,74 V; E°_{Ag+/Ag =} 0,80 V.

soluzione

La Pila è :       Pt | [Fe+3] =[Fe+2] = 0,10 M || [Ag+] = x | Ag

Al Polo positivo+               Ag+ +e- →Ag

E=E° _Ag+/Ag + 0,059 log[Ag+]

al polo negativo     Fe3+ + e- → Fe2+

E polo+= E°_Fe3+/Fe2+ +0,059log[Fe+3]/[Fe+2]   ma essendo [Fe3+]=[Fe2+] =0,1 M
Epolo+ = E°_Fe3+/Fe2+ =0,74 V

Epila= Epolo positivo – Epolonegativo

in questo caso Epila = O=  Epolo positivo – Epolo negativo   da cui  Epolopositivo=Epolo negativo

pertanto      E° _Ag+/Ag + 0,059 log[Ag+]  =  E°_Fe3+/Fe2+ =0,74 V

 log[Ag+] =(E°_Fe3+/Fe2+ – E° _Ag+/Ag) / 0,059

log [Ag+]= 0,74- 0,8/ 0,059 = -10.1 V 

 [Ag+]=10^-10,1=9,7×10^-11 M

9-  La forza elettromotrice della seguente pila a concentrazione:

Ag /AgBr (sol. satura); KBr 0,10 M || AgNO3 0,10 M / Ag

è pari a 0,605 V.

Calcolare la solubilità ed il prodotto di solubilità del bromuro di argento.

soluzione

sia al polo positivo che a quello negativo la reazione è Ag+ +e → Ag

Epolo positivo=E°_Ag+/Ag + + 0,059 log[Ag+]   

Epolo negativo = E°_Ag+/Ag + + 0,059 log[Ag+]/[Ag+]

Epila = Epolo positivo – polo negativo

    Epila = (E°_Ag+/Ag + + 0,059 log[Ag+]   )  – (  E°_Ag+/Ag + + 0,059 log[Ag+])

    Epila = 0,059 log[Ag+]polopositivo /[Ag+]polonegativo

   0,059[Ag+]polonegativo = 0,059log[Ag+]polopositivo – Epila          da cui 

log[Ag+]polo neg = ( 0,059log[Ag+]polopositivo – Epila ) /0,059

log[Ag+]polo neg = ( 0,059 log o,1- 0,605 )/0,059 = 10,3

[Ag+]= 10^-10,3 = 5,0 x 10^-11  M 

AgBr(s) ⇄ Ag+(aq) + Br-(aq)

Kps= [Ag+][Br-]       ma [Br-]=0,1 M

Kps= [Ag+][Br-]=5,0 x  10^-11 x 0,1= 5,0×10-12

11-  A 25° C, la seguente pila ha una f.e.m. di 0,569 V:

Ni/Ni²⁺ 0,250M || Cu2+ 0,050 M/Cu

11Calcolare la costante di equilibrio della reazione di ossidoriduzione che si instaura in tale pila

(R = 0,0821 atm.l.K-1= 8,31 J .K-1 F= 96500 C) .

soluzione

Polo positivo       Cu2+ + 2e- →Cu

Epolo positivo+=E_Cu2+/Cu = E° _Cu2+/Cu + 0,059/2  log[Cu2+]

Polo negativo       Ni2+ + 2e- →Ni                           

Epolo neg=  E_Ni2+/Ni = E°_Ni2+/Ni +0,059/ 2 log[Ni2+]

Epila= Epolo positivo – Epolo negativo

Epila= (E° _Cu2+/Cu + 0,059/2  log[Cu2+]  )  – (  E°_Ni2+/Ni +0,059/ 2 log[Ni2+] )

Epila = E°pila + 0,059/2 log [Cu+2]/[Ni+2]

in questa espressione l’incognita è E°pila che peò può essere calcolata da 

E_pila – 0,059 log [Cu+2]/[Ni+2]

Epila= 0,059/2 log 0,05/0,25

Epila = 0,59V

dalla relazione    -nFEpila = – RTlnKeq  quindi nFEpila=RTlnKeq 

lnKeq= nFEpila/ RT            ln Keq = 2 x 96500 x 0,59 / 8,31 x 298  

lnKeq= 45,98     da cui 

Keq =e ^45,98

Keq= 9,3 x 10¹⁹

12 -una pila ZnSO4 1M || H2/H+x /Pt   ha f.e.m.=0,63 V. Calcolare il PH     E° Zn/Zn+2 =-0,76 V

soluzione

Epila = E polo poitivo- E polo negetivo

Epila= EH2/H+  – E Zn/Zn+2

0,63 = 0,06/2log[H+]² – (-0,76)

0,63- 0,76 = 0,06log[H+]

-0.13/0,06 = log [H+]

PH= -log[H+]= 0,13/0,06 = 2,16

Indicare il valore della f.e.m. (E) di una pila in cui un elettrodo è costituito da una lamina di rame immersa in una soluzione di ioni Cu2+ 2,50 ·10-2 M e l’altro da una lamina di Zn immersa in una soluzione di ioni Zn2+ 1,30 ·10-3 M, entrambi in condizioni standard e a 25 °C. [E°(Cu2+/Cu) = +0,342 V e E°(Zn2+/Zn) = -0,760 V]: A) -1,14 V B) 1,14 V C) 2,30 V D) 1,98 V:

soluzione

lo schema di questa pila è mostrato in figura:

che si scrive:

Zn|[zn+2] 0,0013 M  || 0,025 M Cu+2 | Cu

I potenziali standard di riduzione tabulati sono:

E°(Zn2+/Zn) = -0,760 V

E°(Cu2+/Cu) = +0,342 V

e ricordando che l’ossidante è l’elemento il cui Potenziale di Riduzione Standard è più positivo ( o meno elettronegativo) .

Il potenziale E dell’anodo e del catodo quando [Cu2+]= 2,50 ·10-2 M  e [ Zn2+] 1,30 ·10-3 M è calcolabile dall’equazione di Nernst 

E (Cu2+/Cu) = E° (Cu) + 0.059/2 log 0,025 = 0.34 + 0.030 x – 1,6 = 0,34-0,048 = 0,294 V
E (Zn2+/Zn) = E° (Zn) + 0.059/2 log 0,0013 = – 0.76 – 0.03 x -2,88 = –  0,847 V

pertanto

E_Zn=-0,847 V

E_Cu= 0,294  V

F.E.M = E _catodo – E_anodo = E_Cu   – E_Zn= 0,294-(- 0,847) = 1,141 V

13- Una pila Daniell è costituita da una lamina di zinco immersa in 2 litri di soluzione 0.1M di
ZnSO4 e da una lamina di rame immersa in una soluzione 1M di CuSO4.Calcolare la f.e.m.
iniziale della pila e la sua f.e.m. dopo che ha erogato una corrente costante di 5.1A per 21 ore.
(E°Zn2+/Zn = -0.763 e E°Cu2+/Cu = 0.337)

soluzione

Le reazioni che avvengono agli elettrodi sono:
(-) Zn → Zn2+ + 2e-
(+) Cu2+ + 2e- → Cu
La f.e.m. iniziale della pila è data da:
ΔE = Ec-Ea= ΔE° -0,059/2 x log [Zn+2 ] /[Cu+2] =1,1 – 0,059/2 log 0,1/1 = 1,13 V
Dopo che la pila ha erogato una quantità di elettricità pari a:
5.1 A · 21 h =107.10 A h
la concentrazione dello Zn2+ in soluzione aumenta, ed essendo noto che 1Faraday = 26.8 A · h /eq

   Send article as PDF