FUNZIONE 1 S
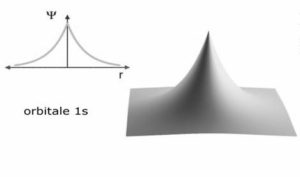
Riferendosi all’atomo di idrogeno si è visto che la funzione d’onda 1S è
1s= ( 1/√π ) x ( 1/a ) ³/² x 1¯ ͬ / ͣ
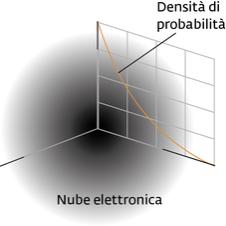
in questo caso si osserva che nella funzione compare solo la variabile r e ciò comporta che la simmetria deve essere sferica nel senso che la densità elettronica è distribuita intorno al nucleo come una sfera.
Consideriamo due sfere concentriche a distanza r ed r+Δr
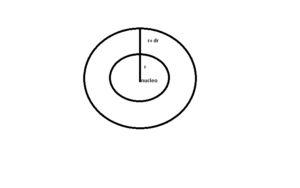poichè la frazione elettronica compresa entro le due sfere corrisponde alla probabilità di trovarvi l’elettrone ΔP occorre elevare al quadrato la funzione 1S nello spazio caratterizzato dalle due sfere (la superficie è 2πr)
ΔP = frazione di elettrone = (1S)² x 4πr² Δr
ΔP = 1/π (1/a)³ x 1¯ ² ͬ / ͣ x 4πr² Δr
semplificando
ΔP = C r² x 1¯ ² ͬ / ͣ Δr
dove C = (1/a)³ x 4
se supponiamo adesso che le due sfere coincidano cioè se si fa in modo che Δr diventi piccolissimo e tenda al valore Zero.
In tal caso il valore di Δp/ Δr tenderà ad un valore limite che rappresenta la densità radiale cioè:
R = C r² x 1¯ ² ͬ / ͣ
se supponiamo che la sfera interna di raggio r diventi sempre più piccola sino a coincidere col nucleo, è ovvio che la frazione di elettrone o meglio la densità radiale compresa tra la sfera esterna r+Δr e quella interna è la più grande possibile pertanto:
dR/dr = C 1¯ ² ͬ / ͣ (2r – 2 r²/a)=0
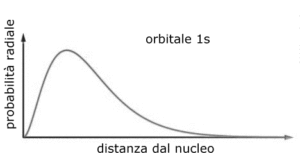
questa è l’espressione matematica che rappresenta la densità elettronica intorno al nucleo per la funzione 1s detta anche orbitale 1S.
Si può osservare che quando r=0 ed r=∝ la funzione si annulla mentre quando r= a si ha un valore massimo di R e quindi la massima densità elettronica si ha ad una distanza dal nucleo pari al raggio di Bohr 0,529167 x A° (1 A°=10-8cm).
La distanza media dell’elettrone dal nucleo mediante l’integrale tra 0 ed ∝
∫ (1S) ² r³ dr
la cui soluzione fornisce il valore medio di r
r = 4/ a³ ∫ 1¯ ² ͬ / ͣ r³ dr = 4/a³( 6 x (a/2)4 = 3/2a
il valore medio è diverso dal valore di r più probabile che invece si è visto è r=a
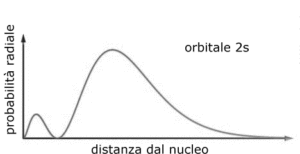
FUNZIONE 2S
LA FUNZIONE è
Per 2s = 1/4(2)1/2 (1/A) 3/2 (r/a -2) 1– r / 2a
anche in questo caso la funzione dipende solo da r e quindi possiede simmetria sferica. Ripetendo il ragionamento seguito per la funzione 1S si ha :
Δp= 4 π² Δr = 1/32π x 1/a3 (r/a-2)2 1-r/a 4π r² Δr
cioè
Δp= C r ² x 1-r/a ( r²/ a² – 4 r/a +4) Δr
LA FUNZIONE 2P
Per quanto riguarda le funzioni 2P si ha
2Px = A senθ cosφ
2Py = A senθ senφ
2Pz = A cosθ
dove
A= 1/4(2π)½ (1/a) 3/2 x r/a 1– r/2a
faremo il calcolo della densità elettronica solo per la funzione 2Pz poichè le altre due funzioni differiscono da questa solo per la direzione nello spazio.
La funzione 2Pz possiede un asse di rivoluzione rappresentato dall’asse Z così come la densità elettronica. Come sii può notare, la differenza tra una funzione di tipo S ed una di tipo P consiste nel fatto che la prima possiede una simmetria sferica nel senso che nessuna direzione spaziale è privilegiata, la seconda invece ha direzioni spaziali privilegiate in particolare Pz è diretto secondo l’asse cartesiano Z, Py secondo l’asse y e Px secondo l’asse x.
Per calcolare la densità elettronica intorno all’asse z o meglio la probabilità di trovare l’elettrone ad una distanza r dal nucleo, eleviamo al quadrato la funzione 2Pz
(2Pz)² = 1/32 1/a³ r² /a² 1-r/a cosθ
a questo punto è bene ricordare gli angoli definiti dagli assi cartesiani.
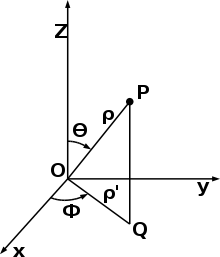
quando θ =0 allora r coincide con l’asse z ed essendo cosθ =1 la densità è
D= 1/32 1/a³ r² /a² 1-r/a
La massima densità si ha quando la derivata di D rispetto ad r è nulla quindi
dD/dr = C r 1-r/a (2-r/a) =0
da cui si deduce che quando r=0 ed r=∝ la densità è nulla mentre assume la massima densità quando r=2a . Quando r=0 il piano si definisce “superficie nodale”
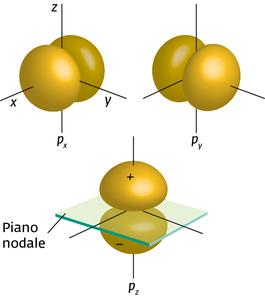
per quanto riguarda gli orbitali d quì forniremo solo le densità
ORBITALI d
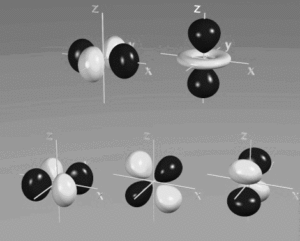
Gli orbitali f sono
